Gọi S là tập hợp tất cả các giá trị nguyên m để đồ thị hàm số y=|3x^4-8x^3-6x^2+24x-m| có 7 điểm cực trị. Tính tổng các phần tử của S.

* Hướng dẫn giải

Phương pháp giải:

Số điểm cực trị của hàm số \[y = \left| {f\left( x \right)} \right|\] với f(x) là hàm đa thức = số điểm cực trị của hàm số y=f(x) + số giao điểm (không tính điểm tiếp xúc) của đồ thị hàm số f(x) và trục hoành.

Giải chi tiết:

Xét hàm số $y=|3x^4-8x^3-6x^2+24x-m|$.

Đồ thị hàm số f(x) có nhiều nhất 3 điểm cực trị và cắt trục hoành tại nhiều nhất 4 điểm.

Do đó để đồ thị hàm số y=|f(x)| có 7 điểm cực trị thì đồ thị hàm số f(x) phải cắt trục hoành tại 4 điểm phân biệt và có 3 điểm cực trị.

đồ thị hàm số f(x) phải cắt trục hoành tại 4 điểm phân biệt (vì khi đó chắc chắn hàm số y=f(x) sẽ có 3 điểm cực trị) ⇒ Phương trình $y=|3x^4-8x^3-6x^2+24x-m|$phải có 4 nghiệm phân biệt.

Xét hàm số g(\[g\left( x \right) = 3{x^4} - 8{x^3} - 6{x^2} + 24x\] ta có $g^{\text{'}}\left(x\right)=12x^3-24x^2-12x+24=0\iff [\begin{array}{l}x=-1\\ x=1\\ x=2\end{array}$.

BBT:

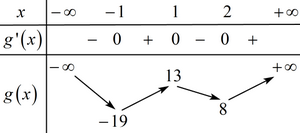
Dựa vào BBT ta thấy phương trình (*) có 4 nghiệm phân biệt $\iff 8<m<13$.

Mà $m\in \mathbb{Z}\Rightarrow m\in S=\{9;10;11;12\}$.

Vậy tổng tất cả các phần tử của S là $9+10+11+12=42$.

Đáp án D.