Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a . Tam SAB giác đều và nằm trong mặt phẳng vuông góc

* Hướng dẫn giải

Phương pháp giải:

- Xác định giao điểm hai trục của hai mặt phẳng (SAB) và (ABCD), chứng minh giao điểm đó chính là tâm mặt cầu ngoại tiếp khối chóp.

- Sử dụng định lí Pytago tính bán kính mặt cầu.

Giải chi tiết:

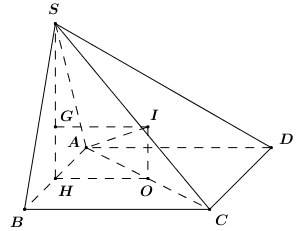
Gọi O là tâm hình vuông ABCD, H là trung điểm của AB, G là trọng tâm ΔSAB.

Vì $\Delta SAB$ đều cạnh a nên $SH\perp AB$ và $SH=\frac{a\sqrt{3}}{2}$.

Ta có: $\{\begin{array}{l}\left(SAB\right)\perp \left(ABCD\right)=AB\\ SH\subset \left(SAB\right);SH\perp AB\end{array}\Rightarrow SH\perp \left(ABCD\right)$.

Kẻ đường d thẳng qua O và song song với SH$\Rightarrow d$ là trục của (ABCD).

CMTT ta có $OH\perp \left(SAB\right)$, kẻ đường thẳng d đi qua G và song song với $OH\Rightarrow d^{\text{'}}\perp \left(SAB\right)$ tại G $\Rightarrow d^{\text{'}}$ là trục của (SAB).

Gọi $I=d\cap d^{\text{'}}$ ta có $\{\begin{array}{l}I\in d\Rightarrow IA=IB=IC=ID\\ I\in d^{\text{'}}\Rightarrow IS=IA=IB\end{array}$, do đó \[IS = IA = IB = IC = ID\] hay I là tâm mặt cầu ngoại tiếp khối chóp S.ABCD, bán kính mặt cầu là R=IA.

Dễ thấy IOHG là hình chữ nhật nên $IO=HG=\frac{1}{3}SH=\frac{1}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{6}$, $OA=\frac{1}{2}AC=\frac{a\sqrt{2}}{2}$.

Áp dụng định lí Pytago trong tam giác vuông \[OIA\] có: $IA=\sqrt{I{O}^2+O{A}^2}=\frac{a\sqrt{21}}{6}$.

Vậy bán kính mặt cầu ngoại tiếp khối chóp S.ABCD là $R=\frac{a\sqrt{21}}{6}$.

Đáp án B.