(VDC): Cho hàm số y=x^4-2mx^2+1, có đồ thị (C) với m là tham số thực. Gọi A là điểm thuộc đồ thị có hoành độ bằng 1.
Câu hỏi :
Cho hàm số , có đồ thị (C) với m là tham số thực. Gọi A là điểm thuộc đồ thị (C) có hoành độ bằng 1. Tìm m để tiếp tuyến Δ với đồ thị (C) tại A cắt đường tròn tạo thành một dây cung có độ dài nhỏ nhất.
A.
B.
C.
D.
* Đáp án
B
* Hướng dẫn giải
Phương pháp giải:
- Tìm tọa độ điểm A, viết phương trình tiếp tuyến của đồ thị hàm số tại A.
- Tìm điểm cố định mà Δ đi qua với mọi m.
- Xác định tâm I và bán kính R của đường tròn .
- Biện luận: Để Δ cắt đường tròn theo một dây cung có độ dài nhỏ nhất thì phải lớn nhất. Sử dụng quan hệ giữa đường vuông góc, đường xiên tìm GTLN của , từ đó tìm m.
Giải chi tiết:
Vì và A có hoành độ bằng 1 nên ta có .
Ta có .
Phương trình tiếp tuyến của (C) tại A là: .
Ta có:
\[\left( \Delta \right):{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {4 - 4m} \right)x - y - 3 + 3m = 0{\mkern 1mu} {\mkern 1mu} \forall m\]
⇒ Đường thẳng Δ luôn đi qua điểm .
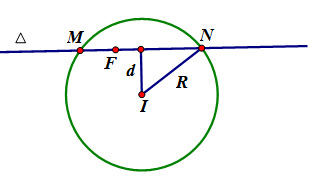
Đường tròn có tâm , bán kính R=2.
Để Δ cắt đường tròn theo một dây cung có độ dài nhỏ nhất thì . phải lớn nhất.
Ta có: (quan hệ đường vuông góc, đường xiên).
.
Ta có: .
.
Vậy để Δ cắt đường tròn tạo thành một dây cung có độ dài nhỏ nhất thì .
Đáp án B.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
[Năm 2022] Đề thi thử môn Toán THPT Quốc gia có đáp án (30 đề) !!
Copyright © 2021 HOCTAP247
