Cho hàm số y=f(x) có đạo hàm liên tục trên R. Đồ thị hàm số f'(x^3+x+2) như hình vẽ sau:Hỏi hàm số có bao nhiêu điểm cực trị?

* Hướng dẫn giải

Chọn D.

* Nhận xét $y=f\left(\left|x\right|\right)$ là hàm số chẵn nên đề thị nhận trục tung Oy làm trục đối xứng, nên ta xét cực trị phải trục Oy

Xét x>0 ta có $y=f\left(\left|x\right|\right)=f\left(x\right)$

* Từ đồ thị hàm số $y=f\text{'}(x^3+x+2)$ ta thấy

$f\text{'}(x^3+x+2)=0\Rightarrow [\begin{array}{l}x\approx -1.5\\ x\approx -\mathrm{0,5}\\ x\approx 0.9\end{array}$

* Xét y=f(x) với x>0

\(y' = f'\left( x \right)\)

Đặt $x=t^3+t+2=(t+1)(t^2-t+2);x>0\Rightarrow t>-1$

Khi đó $y\text{'}=f\text{'}(t^3+t+2)=0\Rightarrow [\begin{array}{l}t\approx 1.5\\ t\approx -\mathrm{0,5}\\ t\approx 0.9\end{array}\Rightarrow [\begin{array}{l}x\approx -2.875<0\\ x\approx 1.375>0\\ x\approx 3.32>0\end{array}$

$\Rightarrow y\text{'}=f\text{'}\left(x\right)$ có 2 nghiệm dương

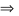đồ thị y=f(x0 có 2 điểm cực trị bên phải Oy.

$\Rightarrow y=f\left(\left|x\right|\right)$ có 5 cực trị (2 cực trị bên phải + 2 cực trị bên trái + 1 giao với trục Oy).