Cho hình lăng trụ ABC.A'B'C' có thể tích là V. Gọi M,N,P là trung điểm các cạnh AA';AB;B'C'. Mặt phẳng

* Hướng dẫn giải

Chọn B.

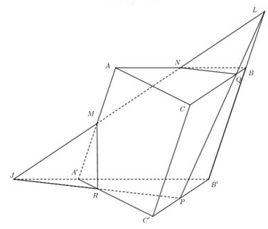
Ta dựng được thiết diện là ngũ giác $MNQPR.$

Đặt \(d\left( {B;\left( {A'B'C'} \right)} \right) = h,A'B' = a,d\left( {C;A'B'} \right) = 2b.\)

Khi đó ta có thể tích lăng trụ $V=\frac{1}{2}.d(C\text{'};A\text{'}B\text{'}).A\text{'}B\text{'}.d[B;(A\text{'}B\text{'}C\text{'})]=\frac{1}{2}.2b.a.h=abh.$

Xét hình chóp $L.JPB\text{'}$ có:

$\frac{LN}{LJ}=\frac{LB}{LB\text{'}}=\frac{NB}{JB\text{'}}=\frac{1}{3}$suy ra $d[L;(A\text{'}B\text{'}C\text{'})]=\frac{3}{2}d[B;(A\text{'}B\text{'}C\text{'})]=\frac{3}{2}h,JB\text{'}=\frac{3}{2}A\text{'}B\text{'}=\frac{3}{2}a,$$d(P;A\text{'}B\text{'})=\frac{1}{2}d(C\text{'};A\text{'}B\text{'})=b.$

Suy ra thể tích khối chóp $L.JPB\text{'}$ là $V_{LJPB\text{'}}=\frac{1}{3}.\frac{3}{2}h.\frac{1}{2}.\frac{3}{2}a.b=\frac{3}{8}abh=\frac{3}{8}V.$

Mặt khác ta có: \(\frac{{{V_{L.NBQ}}}}{{{V_{L.JPB'}}}} = \frac{{LN}}{{LJ}}.\frac{{LB}}{{LB'}}.\frac{{LQ}}{{LP}} = \frac{1}{3}.\frac{1}{3}.\frac{1}{3} = \frac{1}{{27}} \Rightarrow {V_{LNBQ}} = \frac{1}{{27}}{V_{LJPB'}} = \frac{1}{{27}}.\frac{3}{8}V = \frac{1}{{72}}V\)

$\frac{V_{J.RA\text{'}M}}{V_{LJPB\text{'}}}=\frac{JM}{JL}.\frac{JA\text{'}}{JB\text{'}}.\frac{JR}{JP}=\frac{1}{3}.\frac{1}{3}.\frac{1}{2}=\frac{1}{18}\Rightarrow V_{L.NBQ}=\frac{1}{18}{V}_{L.JPB\text{'}}=\frac{1}{18}.\frac{3}{8}V=\frac{1}{48}V.$

Suy ra thể tích khối đa diện $V_{NQBB\text{'}PRA\text{'}}=V_{LJPB\text{'}}-V_{L.NBQ}-V_{J.A\text{'}RM}=\frac{3}{8}V-\frac{1}{72}V-\frac{1}{48}V=\frac{49}{144}V.$