Trang chủ
Đề thi & kiểm tra
Toán học
30 đề thi thử THPT Quốc gia môn Toán năm 2022 có lời giải !!
Cho các số thực thỏa mãn Tìm giá trị nhỏ...
Cho các số thực thỏa mãn Tìm giá trị nhỏ nhất của biểu thức
Câu hỏi :
Cho các số thực thỏa mãn Tìm giá trị nhỏ nhất của biểu thức
A.
B.
C. 1.
D. 0
D.
A. Tập xác định của hàm số là
B. Tập giá trị của hàm số là
C. Tập giá trị của hàm số là
D. Tập xác định của hàm số là
* Đáp án
C
* Hướng dẫn giải
Chọn C.
Điều kiện:
Từ giả thiết ta có:
Xét hàm số trên
Ta có:
Bảng biến thiên:
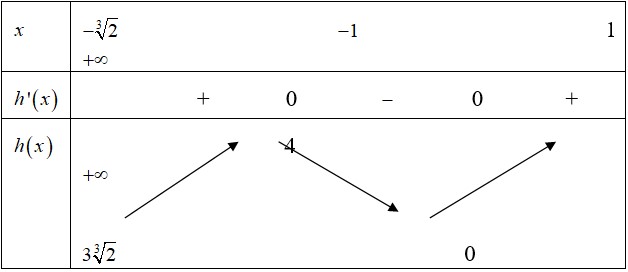
Từ bảng biến thiên suy ra:
Suy ra:
Ta có:
Xét hàm số trên
Ta có:
Ta có:
suy ra hàm số đồng biến trên
Suy ra:
suy ra hàm số đồng biến trên
Vậy Suy ra:
Dấu “=” xảy ra khi và chỉ khi:
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
30 đề thi thử THPT Quốc gia môn Toán năm 2022 có lời giải !!
Số câu hỏi: 81
Copyright © 2021 HOCTAP247
