Trang chủ
Đề thi & kiểm tra
Toán học
30 đề thi thử THPT Quốc gia môn Toán năm 2022 có lời giải !!
Cho tam diện vuông O.ABC có bán kính mặt cầu...
Cho tam diện vuông O.ABC có bán kính mặt cầu ngoại tiếp và nội tiếp lần lượt là R và r
Câu hỏi :
Cho tam diện vuông có bán kính mặt cầu ngoại tiếp và nội tiếp lần lượt là và Khi đó tỉ số đạt giá trị nhỏ nhất là Tính
D.
A. Tập xác định của hàm số là
B. Tập giá trị của hàm số là
C. Tập giá trị của hàm số là
D. Tập xác định của hàm số là
* Đáp án
A
* Hướng dẫn giải
Chọn A.
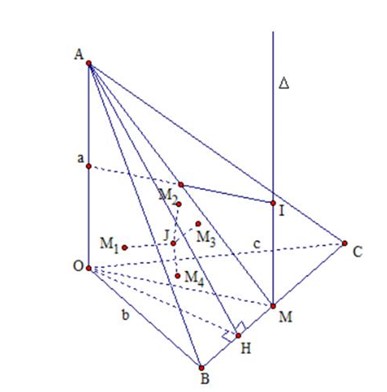
Đặt
Gọi là trung điểm của
dựng trục đường tròn ![]() ngoại tiếp tam giác
ngoại tiếp tam giác
trên mặt phẳng
kẻ đường trung trực của đoạn cắt tại là
tâm mặt cầu ngoại tiếp hình chóp
+)
+) Gọi là chân đường cao hạ từ đỉnh của
tam giác suy ra:
Suy ra:
+) Gọi là tâm mặt cầu nội tiếp hình chóp
Khi đó:
Suy ra:
Vậy Dấu “=” xảy ra khi .
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
30 đề thi thử THPT Quốc gia môn Toán năm 2022 có lời giải !!
Số câu hỏi: 81
Copyright © 2021 HOCTAP247
