Trang chủ
Đề thi & kiểm tra
Toán học
Đề minh họa THPT Quốc gia môn Toán năm 2022 chọn lọc, có lời giải (30 đề) !!
Gọi (H) là hình phẳng giới hạn bởi đồ thị...
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số: y=x^2-4x+4 , trục tung
Câu hỏi :
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số: , trục tung và trục hoành. Xác định k để đường thẳng (d) đi qua điểm có hệ số góc k chia (H) thành hai phần có diện tích bằng nhau.
A.
B.
C.
D.
* Đáp án
* Hướng dẫn giải
Phương trình hoành độ giao điểm của đồ thị hàm số và trục hoành là: .
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số: , trục tung và trục hoành là: .
Phương trình đường thẳng (d) đi qua điểm
có hệ số góc k có dạng: .
Gọi B là giao điểm của (d) và trục hoành. Khi đó .
Đường thẳng (d) chia (H) thành hai phần có diện tích
bằng nhau khi và .
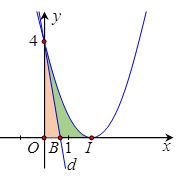
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số: , trục tung và trục hoành là: .
Phương trình đường thẳng (d) đi qua điểm
có hệ số góc k có dạng: .
Gọi B là giao điểm của (d) và trục hoành. Khi đó .
Đường thẳng (d) chia (H) thành hai phần có diện tích
bằng nhau khi và .
Chọn đáp án C
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề minh họa THPT Quốc gia môn Toán năm 2022 chọn lọc, có lời giải (30 đề) !!
Số câu hỏi: 1483
Copyright © 2021 HOCTAP247
