Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2a. Cạnh bên SA vuông góc với mặt phẳng đáy (ABCD).

* Hướng dẫn giải

Đáp án A.

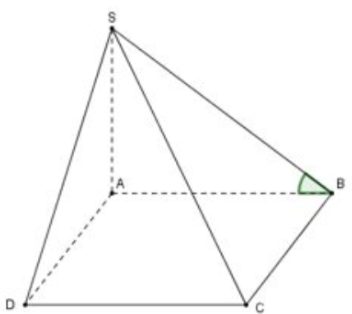
Ta có \(\left\{ \begin{array}{l}BC \bot AB\left( 1 \right)\\BC \bot SA\end{array} \right. \Rightarrow BC \bot SB\left( 2 \right).\)

Từ (1) và (2) suy ra góc giữa mặt phẳng \(\left( {SBC} \right)\) và mặt đáy \(\left( {ABCD} \right)\) là góc \(\widehat {SBA}\), kết hợp giả thiết suy ra \(\widehat {SBA} = {60^0}.\)

Xét tam giác vuông \(SAB\) ta có \(\tan {60^0} = \frac{{SA}}{{AB}} \Rightarrow SA = AB.\tan {60^0} = 2a\sqrt 3 .\)

Thể tích của khối chóp \(S.ABCD\) là \(V = \frac{1}{3}.Bh = \frac{1}{3}{S_{ABCD}}.SA = \frac{1}{3}{\left( {2a} \right)^2}2a\sqrt 3 = \frac{{8{a^3}\sqrt 3 }}{3}.\)