Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,BC = 2a,BA = a sqrt 3 . Biết tam giác SAB vuông tại A,

* Hướng dẫn giải

Đáp án C.

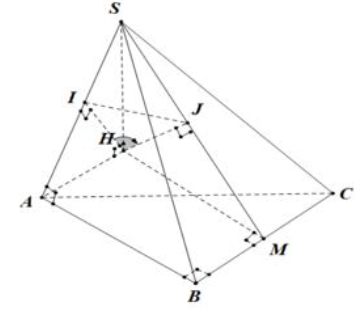
+ Gọi \(M\) là trung điểm của \(BC,\) dựng hình chữ nhật \(ABMH\)

Khi đó \(\left\{ \begin{array}{l}AB \bot SH\\BC \bot SH\end{array} \right. \Rightarrow SH \bot \left( {ABC} \right)\)

Kẻ \(HI \bot SA \Rightarrow HI \bot \left( {SAB} \right).\)

\(HJ \bot SM \Rightarrow HJ \bot \left( {SBC} \right)\)

\( \Rightarrow \left( {\left( {SAB} \right),\left( {SBC} \right)} \right) = \angle IHJ.\)

+ Đặt \(SH = x \Rightarrow HI = \frac{{ax}}{{\sqrt {{a^2} + {x^2}} }};HJ = \frac{{a\sqrt 3 a}}{{\sqrt {3{a^2} + {x^2}} }};SI = \frac{{{x^2}}}{{\sqrt {{a^2} + {x^2}} }};SJ = \frac{{{x^2}}}{{\sqrt {3{a^2} + {x^2}} }}.\)

\(\cos ASM = \frac{{{x^2}}}{{\sqrt {{a^2} + {x^2}} .\sqrt {3{a^2} + {x^2}} }};I{J^2} = S{I^2} + S{J^2} - 2SI.SJ.\cos ASM = \frac{{4{a^2}{x^4}}}{{\left( {{a^2} + {x^2}} \right)\left( {3{a^2} + {x^2}} \right)}}\)

\(\sin \varphi = \sqrt {\frac{{20}}{{21}}} \Rightarrow \cos \varphi = \sqrt {\frac{1}{{21}}} .\)

\(\cos \varphi = \frac{{H{I^2} + H{J^2} - I{J^2}}}{{2HI.HJ}}\)

\( \Leftrightarrow \frac{2}{{\sqrt {21} }}.\frac{{ax}}{{\sqrt {{a^2} + {x^2}} }}.\frac{{a\sqrt 3 a}}{{\sqrt {3{a^2} + {x^2}} }} = \frac{{{a^2}{x^2}}}{{{a^2} + {x^2}}} + \frac{{3{a^2}{x^2}}}{{3{a^2} + {x^2}}} - \frac{{4{a^2}{x^4}}}{{\left( {{a^2} + {x^2}} \right)\left( {3{a^2} + {x^2}} \right)}}\)

\( \Leftrightarrow \frac{2}{{\sqrt 7 }}\sqrt {{a^2} + {x^2}} .\sqrt {3{a^2} + {x^2}} = 6{a^2} \Leftrightarrow x = a\sqrt 6 .\)

\({V_{S.ABC}} = \frac{1}{3}SH.{S_{ABC}} = {a^3}\sqrt 2 .\)