Trang chủ
Đề thi & kiểm tra
Toán học
[Năm 2022] Đề thi thử môn Toán THPT Quốc gia có đáp án (30 đề) !!
Khoảng nghịch biến của hàm số y = x^3 -...
Khoảng nghịch biến của hàm số y = x^3 - 3x + 3 là (a;b) thì P = a^2 - 2ab bằng
Câu hỏi :
Khoảng nghịch biến của hàm số \(y = {x^3} - 3x + 3\) là \(\left( {a;b} \right)\) thì \(P = {a^2} - 2ab\) bằng
A.\(P = 4.\)
B.\(P = 1.\)
C.\(P = 3.\)
D. \(P = 2.\)
* Đáp án
C
* Hướng dẫn giải
Đáp án C.
Tập xác định \(D = \mathbb{R}.\)
\(y' = 3{x^2} - 3\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\)
BBT
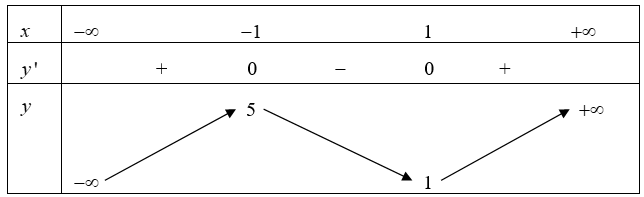
\( \Rightarrow \) Hàm số nghịch biến trên khoảng \(\left( { - 1;1} \right)\) do đó \(a = - 1;b = 1\)
\( \Rightarrow P = {\left( { - 1} \right)^2} - 2.\left( { - 1} \right).1 = 3\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
[Năm 2022] Đề thi thử môn Toán THPT Quốc gia có đáp án (30 đề) !!
Số câu hỏi: 1497
Copyright © 2021 HOCTAP247
