Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC vuông tại A,AB = a sqrt 3 ,AC = AA' = a. Sin góc giữa đường thẳng

* Hướng dẫn giải

Đáp án B.

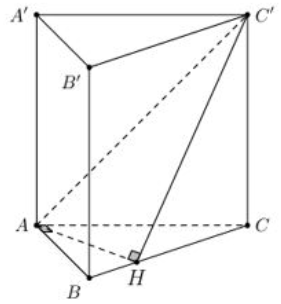
Trong mặt phẳng \(\left( {ABC} \right)\) kẻ \(AH \bot BC\) với \(H \in BC.\)

Do \(BB' \bot \left( {ABC} \right) \Rightarrow BB' \bot AH.\) Suy ra \(AH \bot \left( {BCC'B'} \right).\)

Khi đó góc giữa đường thẳng \(AC'\) và mặt phẳng \(\left( {BCC'B'} \right)\) là góc giữa đường thẳng \(AC'\) và đường thẳng \(HC'\) hay là góc \(\widehat {AC'H}.\)

Ta có \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {3{a^2} + {a^2}} = 2a;AC' = AC\sqrt 2 = a\sqrt 2 \)

Khi đó trong tam giác \(ABC\) vuông tại \(A\) ta có:

\(AH.BC = AB.AC \Leftrightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{a\sqrt 3 .a}}{{2a}} = \frac{{a\sqrt 3 }}{2}.\)

Trong tam giác \(AHC'\) vuông tại \(H\) ta có: \(\sin \widehat {AC'H} = \frac{{AH}}{{AC'}} = \frac{{\frac{{a\sqrt 3 }}{2}}}{{a\sqrt 2 }} = \frac{{\sqrt 6 }}{4}.\)