Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, cạnh bên bằng 3a. Tính thể tích V của hình chóp đã cho.

* Hướng dẫn giải

Đáp án C.

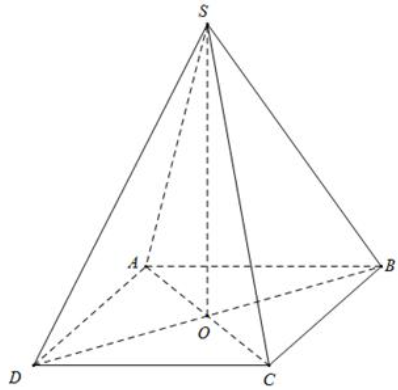
Gọi \(O = AC \cap BD.\)

Vì \(S.ABCD\) là hình chóp tứ giác đều nên \(SO \bot \left( {ABCD} \right).\)

Theo bài ra ta có: \(OA = \frac{1}{2}AC = a\sqrt 2 .\)

Xét tam giác \(SOA\) vuông tại \(O\) ta có: \(SO = \sqrt {S{A^2} - O{A^2}} = \sqrt {{{\left( {3a} \right)}^2} - {{\left( {a\sqrt 2 } \right)}^2}} = a\sqrt 7 .\)

Diện tích hình vuông \(ABCD\) bằng: \({S_{ABCD}} = {\left( {2a} \right)^2} = 4{a^2}.\)

Thể tích của khối chóp \(S.ABCD\) bằng: \({V_{S.ABCD}} = \frac{1}{3}.SO.{S_{ABCD}} = \frac{1}{3}.a\sqrt 7 .4{a^2} = \frac{{4\sqrt 7 {a^3}}}{3}.\)