Cho phương trình 27^x + 3x*9^x + (3(x^2) + 1)*3^x =(m^3-1)*x^3 + (m-1)x, m là tham số. Biết rằng giá trị m nhỏ nhất để phương

* Hướng dẫn giải

Đáp án A.

Phương trình đã cho tương đương

\({\left( {{3^x}} \right)^3} + 3x.{\left( {{3^x}} \right)^2} + \left( {3{x^2} + 1} \right){.3^x} = \left( {{m^3} - 1} \right){x^3} + \left( {m - 1} \right)x\)

\( \Leftrightarrow {\left( {{3^x} + x} \right)^3} + {3^x} + x = {\left( {mx} \right)^3} + mx\left( * \right)\)

Xét hàm số \(f\left( u \right) = {u^3} + u,f'\left( u \right) = 3{u^2} + 1 >0,\forall u \in \mathbb{R}.\)

Phương trình (*) tương đương \(f\left( {{3^x} + x} \right) = f\left( {mx} \right)\)

Nên \({3^x} + x = mx \Leftrightarrow m = \frac{{{3^x}}}{x} + 1,x >0.\)

Xét hàm số \(g\left( x \right) = \frac{{{3^x}}}{x} + 1,x >0.\)

Ta có \(g'\left( x \right) = \frac{{{3^x}\left( {x\ln 3 - 1} \right)}}{{{x^2}}} \Rightarrow g'\left( x \right) = 0 \Leftrightarrow x = {\log _3}e.\)

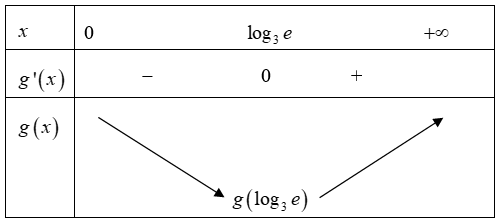
Phương trình có nghiệm khi và chỉ khi \(m \ge g\left( {{{\log }_3}e} \right) = 1 + e\ln 3 \Rightarrow \left\{ \begin{array}{l}x = 1\\b = 3\end{array} \right..\)