Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích V. Gọi E là điểm trên cạnh SC sao cho EC = 2ES.

* Hướng dẫn giải

Đáp án D.

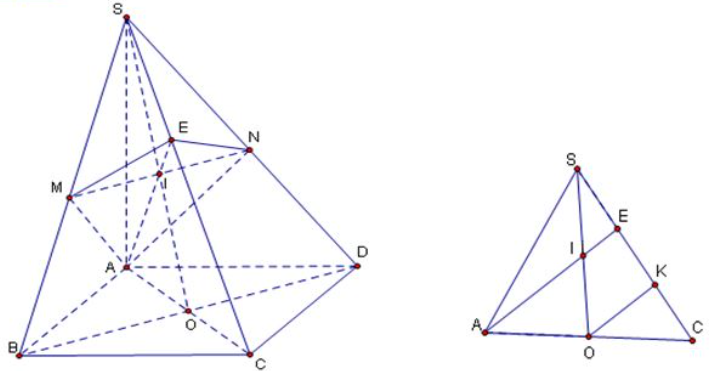
Gọi \(O\) là tâm của hình bình hành \(ABCD.\)

Trong \(\left( {SAC} \right).\) Gọi \(I = SO \cap AE.\)

Từ \(I,\) kẻ đường thẳng song song với đường thẳng \(BD\) cắt hai cạnh \(SB,SD\) lần lượt tại \(M,N.\)

Gọi \(K\) là trung điểm \(EC \Rightarrow SE = EK = KC.\)

Do \(OK\) là đường trung bình của tam giác \(CAE \Rightarrow OK//IE \Rightarrow \frac{{SI}}{{SO}} = \frac{{SE}}{{SK}} = \frac{1}{2}.\)

Do \(MN//BD \Rightarrow \frac{{SM}}{{SB}} = \frac{{SN}}{{SD}} = \frac{{SI}}{{SO}} = \frac{1}{2}\)

Ta có: \({V_{S.AMBN}} = {V_{S.AMB}} + {V_{S.ABN}}.\)

\(\frac{{{V_{S.AME}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SB}}.\frac{{SE}}{{SC}} = \frac{1}{2}.\frac{1}{3} = \frac{1}{6} \Rightarrow {V_{S.AME}} = \frac{1}{6}{V_{S.ABC}}.\)

\(\frac{{{V_{S.ANE}}}}{{{V_{S.ADC}}}} = \frac{{SN}}{{SD}}.\frac{{SE}}{{SC}} = \frac{1}{2}.\frac{1}{3} = \frac{1}{6} \Rightarrow {V_{S.ANE}} = \frac{1}{6}{V_{S.ACD}}.\)

\({V_{S.AMBN}} = {V_{S.AMB}} + {V_{S.ABN}} = \frac{1}{6}\left( {{V_{S.ABC}} + {V_{S.ACD}}} \right) = \frac{1}{6}{V_{S.ABCD}}.\)

\( \Rightarrow {V_{S.AMBN}} = \frac{1}{6}V.\)