Cho tứ diện đều ABCD có cạnh bằng a. Gọi M,N lần lượt là trọng tâm các tam giác ABD,ABC và E là điểm đối xứng

* Hướng dẫn giải

Đáp án A.

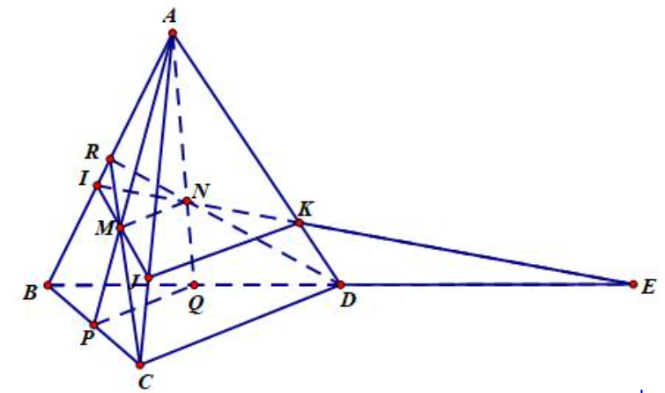
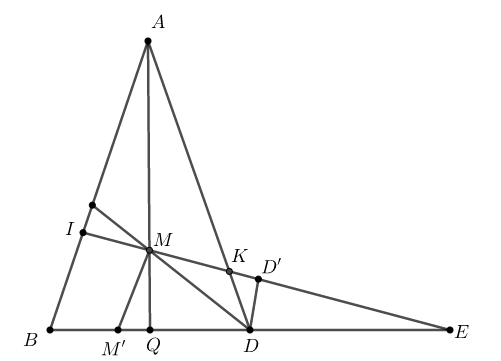
Xét mặt phẳng chứa tam giác \(ABD\). Gọi \(D'\) trên \(IE\) sao cho \[DD'//AQ\] ta có: \(\frac{{DD'}}{{MQ}} = \frac{{ED}}{{EQ}} = \frac{2}{3}\)

Mà \(\Delta KDD' \sim \Delta KAM \Rightarrow \frac{{KD}}{{KA}} = \frac{{DD'}}{{AM}} = \frac{{DD'}}{{2MQ}} = \frac{1}{3}\)

Gọi \(M'\) trên \(BD\) sao cho \(MM'//AB.\) Ta có:

\(M'Q = \frac{1}{3}BQ = \frac{1}{3}.\frac{1}{4}BE = \frac{1}{{12}}BE \Rightarrow EM' = 3EQ + QM' = \left( {\frac{3}{4} + \frac{1}{{12}}} \right)BE = \frac{5}{6}BE\)

\( \Rightarrow \frac{{MM'}}{{IB}} = \frac{{EM'}}{{EB}} = \frac{5}{6} \Rightarrow MM' = \frac{5}{6}IB\)

Xét mặt tam giác \(ABQ\). Ta có \(\frac{{MM'}}{{AB}} = \frac{{QM}}{{QA}} = \frac{1}{3} \Rightarrow \frac{5}{6}\frac{{IB}}{{AB}} = \frac{1}{3} \Rightarrow \frac{{IB}}{{AB}} = \frac{2}{5} \Rightarrow \frac{{AI}}{{AB}} = \frac{3}{5}\)

Vì \(MN//PQ//CD \Rightarrow MN//\left( {ACD} \right) \Rightarrow MN//JK//CD \Rightarrow \frac{{AJ}}{{AC}} = \frac{{AK}}{{AD}} = \frac{3}{4}\)

Vì \(ABCD\) là tứ diện đều có cạnh bằng \(a \Rightarrow {V_{ABCD}} = \frac{{{a^3}\sqrt 2 }}{{12}}\)

Ta lại có: \(\frac{{{V_{AIJK}}}}{{{V_{ABCD}}}} = \frac{{AI}}{{AB}}.\frac{{AJ}}{{AC}}.\frac{{AK}}{{AD}} = \frac{3}{5}.\frac{3}{4}.\frac{3}{4} = \frac{{27}}{{80}} \Rightarrow {V_{AIJK}} = \frac{{27}}{{80}}{V_{ABCD}} = \frac{{27}}{{80}}\frac{{{a^3}\sqrt 2 }}{{12}} = \frac{{9\sqrt 2 {a^3}}}{{320}}\)