Cho một tấm nhôm hình vuông cạnh 6cm. Người ta muốn cắt một hình thang như hình vẽ. Trong đó AE=2cm

* Hướng dẫn giải

Đáp án C.

Hai tam giác \(AHE\) và \(CFG\) đồng dạng suy ra: \(\frac{{CG}}{{AE}} = \frac{{CF}}{{AH}} \Leftrightarrow \frac{y}{2} = \frac{3}{x} \Leftrightarrow xy = 6.\)

Ta có: \({S_{EFGH}} = {S_{ABCD}} - {S_{AHE}} - {S_{BEF}} - {S_{CFG}} - {S_{DGH}}\)

\( = 36 - \frac{1}{2}.2x - \frac{1}{2}.4.3 - \frac{1}{2}.3.y - \frac{1}{2}.\left( {6 - x} \right).\left( {6 - y} \right)\)

\( = 36 - x - 6 - \frac{3}{2}.y - \frac{1}{2}.\left( {36 - 6\left( {x + y} \right) + xy} \right)\)

\( = 36 - x - 6 - \frac{3}{2}.y - \frac{1}{2}.\left( {36 - 6\left( {x + y} \right) + 6} \right) = 9 + 2x + \frac{3}{2}y\)

Với \(y = \frac{6}{x},\) ta có: \({S_{EFGH}} = 9 + 2x + \frac{9}{x}.\)

Xét hàm số \(f\left( x \right) = 9 + 2x + \frac{9}{x},\) trên khoảng \(\left( {0;6} \right)\) ta có: \(f'\left( x \right) = 2 - \frac{9}{{{x^2}}},\) \(f'\left( x \right) = 0 \Leftrightarrow 2 - \frac{9}{{{x^2}}} = 0 \Rightarrow x = \frac{{3\sqrt 2 }}{2}.\)

Ta có bảng biến thiên:

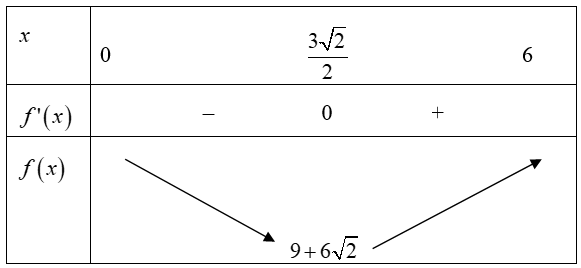
Từ bảng biến thiên suy ra: \({\min _{{S_{EFGH}}}} = \mathop {\min }\limits_{\left( {0;6} \right)} f\left( x \right) = 9 + 6\sqrt 2 \) khi \(x = \frac{{3\sqrt 2 }}{2} \Rightarrow y = 2\sqrt 2 .\)