Cho hình nón (N) có đỉnh S bán kính đáy r = 1 và độ dài đường sinh l = 2 căn 2 . Mặt cầu đi qua S và đường tròn đáy của

* Hướng dẫn giải

Đáp án A.

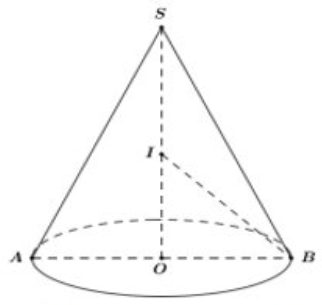
Gọi \(I\) là tâm của mặt cầu đi qua \(S\) và đường thẳng đáy của \(\left( N \right).\)

\(R\) là bán kính của mặt cầu cần tìm.

Theo giả thiết, ta có \(SO = \sqrt {{l^2} - {r^2}} = \sqrt 7 .\)

Trường hợp 1. \(IO = SO - R = \sqrt 7 - R.\)

Trong tam giác vuông \(IOB,\) ta có \(I{B^2} = I{O^2} + O{B^2} \Leftrightarrow {R^2} = {\left( {\sqrt 7 - R} \right)^2} + 1 \Leftrightarrow R = \frac{{4\sqrt 7 }}{7}.\)

Trường hợp 2. \(IO = R - SO = R - \sqrt 7 .\)

Trong tam giác vuông \(IOB,\) ta có \(I{B^2} = I{O^2} + O{B^2} \Leftrightarrow {R^2} = {\left( {R - \sqrt 7 } \right)^2} + 1 \Leftrightarrow R = \frac{{4\sqrt 7 }}{7}.\)