Cho hình chóp S.ABCD có đáy là hình vuông và có mặt phẳng SAB vuông góc với mặt phẳng đáy, tam giác SAB

* Hướng dẫn giải

Đáp án D.

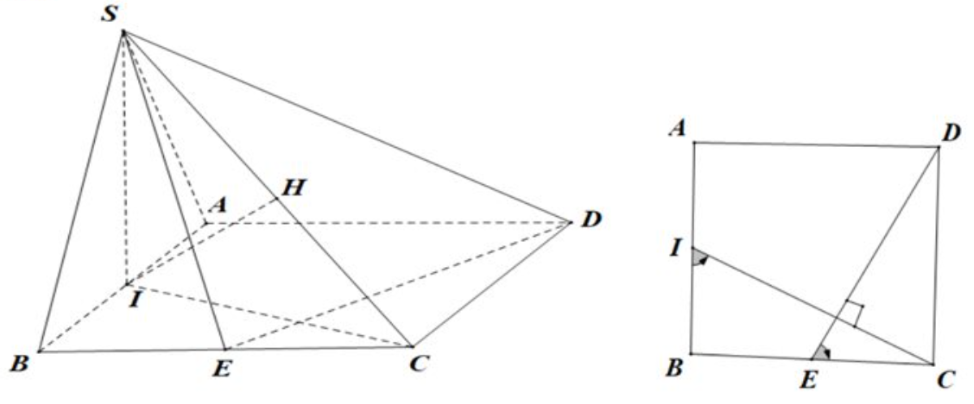
+ \(\left\{ \begin{array}{l}DE \bot IC\\DE \bot SI\end{array} \right. \Rightarrow DE \bot \left( {SIC} \right) \Rightarrow \left( {SIC} \right) \bot \left( {SDE} \right).\) Suy ra A đúng/

+ \(\left\{ \begin{array}{l}BC \bot AI\\BC \bot AB\end{array} \right. \Rightarrow BC \bot \left( {SAI} \right) \Rightarrow \left( {SBC} \right) \bot \left( {SAI} \right).\) Suy ra B đúng

+ \(DE \bot \left( {SCI} \right);BC \bot \left( {SAI} \right)\) nên \(\left( {\left( {SIC} \right),\left( {SAB} \right)} \right) = \left( {BC,DE} \right) = \angle DEC = \angle BIC.\)

Suy ra D sai.

Vậy D sai.