Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 3,BC = 4,SA = 2. Tam giác SAC nằm trong mặt phẳng
Câu hỏi :
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, \[AB = 3,BC = 4,SA = 2\]. Tam giác SAC nằm trong mặt phẳng vuông góc với đáy và có diện tích bằng 4. Côsin của góc giữa hai mặt phẳng (SAB) và (SAC) bằng
A.\[\frac{{3\sqrt {17} }}{{17}}\].
B.\[\frac{{5\sqrt {34} }}{{17}}\].
C.\[\frac{{2\sqrt {34} }}{{17}}\].
D. \[\frac{{3\sqrt {34} }}{{34}}\].
* Đáp án
D
* Hướng dẫn giải
Đáp án D.
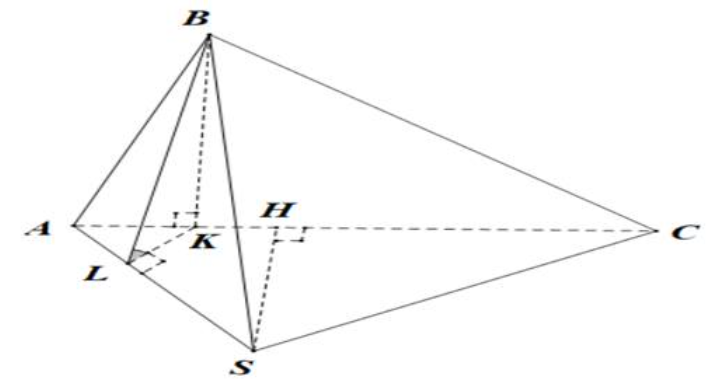
TH1: \(H\) thuộc đoạn thẳng \(AC.\)
+ Kẻ \(SH \bot AC \Rightarrow SH \bot \left( {ABCD} \right)\) mặt khác \({S_{\Delta SAC}} = \frac{1}{2}SH.AC = 4 \Leftrightarrow SH = \frac{8}{5}\)
\(AH = \frac{6}{5};\sin \widehat {SAC} = \frac{{SH}}{{SA}} = \frac{4}{5}.\)
+ Kẻ \(BK \bot AC \Rightarrow BK \bot \left( {SAC} \right)\) kẻ \(KL \bot SA \Rightarrow SA \bot \left( {BKL} \right) \Rightarrow \left( {\left( {SAB} \right),\left( {SBC} \right)} \right) = \widehat {BLK}\)
Ta có: \(\frac{1}{{B{K^2}}} = \frac{1}{{B{A^2}}} + \frac{1}{{B{C^2}}} \Rightarrow BK = \frac{{12}}{5}\) và \(AK = \frac{9}{5};KL = AK.\sin \widehat {SAC} = \frac{{36}}{{25}}\)
\(BL = \frac{{12\sqrt {34} }}{{25}};\cos \widehat {BLK} = \frac{{KL}}{{BL}} = \frac{{3\sqrt {34} }}{{34}}\)
TH2. \(H\) không thuộc đoạn thẳng \(AC.\)
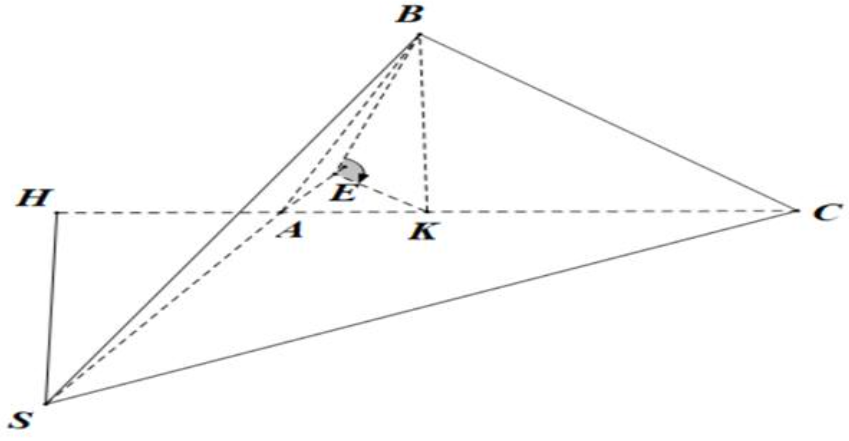
+ Kẻ \(SH \bot AC \Rightarrow SH \bot \left( {ABCD} \right)\) mặt khác \({S_{\Delta SAC}} = \frac{1}{2}SH.AC = 4 \Leftrightarrow SH = \frac{8}{5}\)
\(AH = \frac{6}{5};\sin \widehat {SAH} = \frac{{SH}}{{SA}} = \frac{4}{5}.\)
+ Kẻ \(BK \bot AC \Rightarrow BK \bot \left( {SAC} \right)\) kẻ \(KE \bot SA \Rightarrow \left( {\left( {SAB} \right),\left( {SBC} \right)} \right) = \widehat {BEK}\)
Ta có: \(\frac{1}{{B{K^2}}} = \frac{1}{{B{A^2}}} + \frac{1}{{B{C^2}}} \Rightarrow BK = \frac{{12}}{5}\) và \(AK = \frac{9}{5};KE = AK.\sin \widehat {SAH} = \frac{{36}}{{25}}\)
\(BE = \frac{{12\sqrt {34} }}{{25}};\cos \widehat {BEK} = \frac{{KL}}{{BL}} = \frac{{3\sqrt {34} }}{{34}}\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
[Năm 2022] Đề thi thử môn Toán THPT Quốc gia có đáp án (30 đề) !!
Copyright © 2021 HOCTAP247
