Tìm tất cả các giá trị thực của tham số m để hàm số y = 3*(cosx)^4 + 3/2*(sinx)^2 + mcosx -5/2 đồng biến trên

* Hướng dẫn giải

Đáp án A.

\(y = 3{\cos ^4}x + \frac{3}{2}{\sin ^2}x + m\cos x - \frac{5}{2} \Leftrightarrow y = 3{\cos ^4}x - \frac{3}{2}{\cos ^2}x + m\cos x - 1\)

Đặt \(t = \cos x.\) Vì \(x \in \left( {\frac{\pi }{3};\frac{{2\pi }}{3}} \right]\) nên \(t \in \left[ { - \frac{1}{2};\frac{1}{2}} \right).\)

Hàm số trở thành \(f\left( t \right) = 3{t^4} - \frac{3}{2}{t^2} + mt - 1,f'\left( t \right) = 12{t^3} - 3t + m\)

Yêu cầu bài toán \( \Leftrightarrow f\left( t \right)\) nghịch biến trên \(\left[ { - \frac{1}{2};\frac{1}{2}} \right) \Leftrightarrow f'\left( t \right) \le 0,\forall t \in \left[ { - \frac{1}{2};\frac{1}{2}} \right)(f'\left( t \right) = 0\) chỉ tại một số điểm) \( \Leftrightarrow 12{t^3} - 3t + m \le 0{\rm{ }}\forall t \in \left[ { - \frac{1}{2};\frac{1}{2}} \right) \Leftrightarrow m \le - 12{t^3} + 3t{\rm{ }}\forall t \in \left[ { - \frac{1}{2};\frac{1}{2}} \right)\)

Đặt \(g\left( t \right) = - 12{t^3} + 3t,g'\left( t \right) = - 36{t^2} + 3,g'\left( t \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t = \frac{{\sqrt 3 }}{6} \in \left[ { - \frac{1}{2};\frac{1}{2}} \right)\\t = - \frac{{\sqrt 3 }}{6} \in \left[ { - \frac{1}{2};\frac{1}{2}} \right)\end{array} \right.\)

Ta có

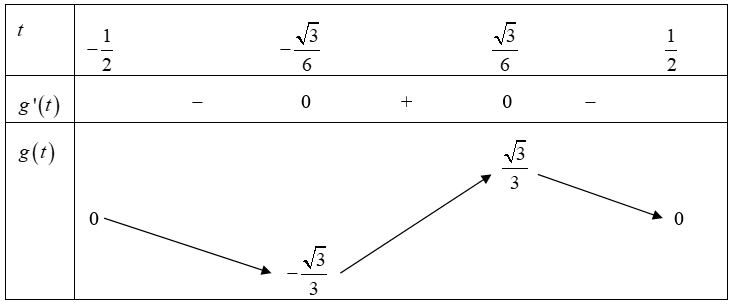
Dựa vào bảng biến thiên \(m \le - \frac{{\sqrt 3 }}{3}.\)