Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác cân có AB = BC = 3a. Đường thẳng A'C tạo với đáy một góc

* Hướng dẫn giải

Đáp án C.

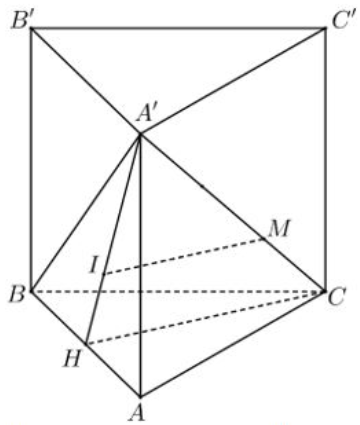
Hình lăng trụ đứng \(ABC.A'B'C' \Rightarrow A\) là hình chiếu của \(A'\) trên mặt đáy \(\left( {ABC} \right)\)

\( \Rightarrow \widehat {A'CA} = \left( {\widehat {A'C,\left( {ABC} \right)}} \right) = \widehat {A'CA} = {60^0}\)

\(\Delta A'CA\) vuông tại \(A \Rightarrow A'A = AC.\tan \widehat {A'CA} = 3a.\tan {60^0} = 3a\sqrt 3 \)

\(\Delta A'AB\) vuông tại \(A \Rightarrow AB = \sqrt {A'{B^2} - A'{A^2}} = \sqrt {{{\left( {a\sqrt {31} } \right)}^2} - {{\left( {3a\sqrt 3 } \right)}^2}} = \sqrt {4{a^2}} = 2a\)

Kẻ \(CH \bot AB\) tại \(H \Rightarrow H\) là trung điểm của \(AB\) (do \(\Delta ABC\) cân tại \(C)\)

Mà \(A'A \bot \left( {ABC} \right) \Rightarrow A'A \bot CH \Rightarrow CH \bot \left( {ABB'A'} \right)\)

Kẻ \(MI//CH,I \in A'H \Rightarrow MI \bot \left( {ABB'A'} \right) \Rightarrow MI\) là khoảng cách từ \(M\) tới \(mp\left( {ABB'A'} \right)\)

Ta có: \(HA = \frac{{AB}}{2} = \frac{{2a}}{2} = a \Rightarrow CH = \sqrt {A{C^2} - H{A^2}} = \sqrt {{{\left( {3a} \right)}^2} - {a^2}} = \sqrt {8{a^2}} = 2a\sqrt 2 \)

\(MI//HC \Rightarrow \frac{{MI}}{{HC}} = \frac{{A'M}}{{AC}},\) mà \(A'M = 2MC \Rightarrow \frac{{A'M}}{{AC}} = \frac{2}{3} \Rightarrow \frac{{MI}}{{HC}} = \frac{2}{3}\)

\( \Rightarrow MI = \frac{2}{3}HC = \frac{2}{3}.2a\sqrt 2 = \frac{{4a\sqrt 2 }}{3}\)

Vậy khoảng cách từ \(M\) đến mặt phẳng \(\left( {ABB'A'} \right)\) là \(\frac{{4a\sqrt 2 }}{3}.\)