Trong không gian Oxyz cho ba đường thẳng , . Mặt phẳng với nguyên dương, đi qua và cắt 3 đường thẳng trên tại ba điểm lả ba đỉnh

Phương pháp giải:

- Xác định các VTCP của ${\text{d}}_1, {\text{d}}_2, {\text{d}}_3$ lần lượt là ${\text{u}}_1,{\text{u}}_2,{\text{u}}_3$.

- Chứng minh 3 đường thẳng đã cho đôi một vuông góc và đồng quy tại .

- Chứng minh chóp ABCD là chóp tam giác đều.

- Gọi H là trọng tâm tam giác ABC, chứng minh $\overrightarrow{\text{n}}=\overrightarrow{\text{AB}}+\overrightarrow{\text{AC}}+\overrightarrow{\text{AD}}$ là một VTPT của (P).

- Giải hệ $\overrightarrow{{\text{n}}_{\text{P}}}=\text{k}\left(\overrightarrow{{\text{u}}_1}\pm \overrightarrow{{\text{u}}_2}\pm \overrightarrow{{\text{u}}_3}\right)$, thử các trường hợp tìm . Từ đó suy ra phương trình mặt phẳng (P) và xác định điểm thuộc (P).

Giải chi tiết:

Ta có các VTCP của ${\text{d}}_1, {\text{d}}_2, {\text{d}}_3$ lần lượt là: $\overrightarrow{{\text{u}}_1}=(2;2;1),\overrightarrow{{\text{u}}_2}=(1;-2;2),\overrightarrow{{\text{u}}_3}=(2;-1;-2)$.

Ta có: $\overrightarrow{{\text{u}}_1}.\overrightarrow{{\text{u}}_2}=\overrightarrow{{\text{u}}_2}.\overrightarrow{{\text{u}}_3}=\overrightarrow{{\text{u}}_1}.\overrightarrow{{\text{u}}_3}=0$

Suy ra ba đường thẳng đã cho đôi một vuông góc.

Lại có $\text{A}(1;-1;1)$ nằm trên cả ba đường thẳng đã cho, nên chúng đồng quy tại .

Vì $\text{M}\in \left(\text{P}\right)\iff 2\text{a}+\text{c}-1=0\iff \text{c}=1-2\text{a}$, suy ra (P) nhận $\overrightarrow{n_{\text{P}}}=(\text{a};\text{b};1--2\text{a})$ làm VTPT.

Giả sử (P) cắt ba đường thẳng đã cho lần lượt tại B, C, D thì tam giác BCD đều.

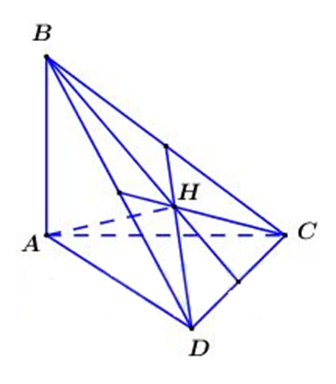
Khi đó ABCD là tứ diện vuông, chóp ABCD là chóp đều.

Gọi H là trọng tâm tam giác $\text{BCD}\Rightarrow \text{AH}\perp \left(\text{BCD}\right)$ hay $\text{AH}\perp \left(\text{P}\right)$ và $\overrightarrow{\text{AH}}=\frac{1}{3}(\overrightarrow{\text{AB}}+\overrightarrow{\text{AC}}+\overrightarrow{\text{AD}})$.

$\Rightarrow \overrightarrow{\text{n}}=\overrightarrow{\text{AB}}+\overrightarrow{\text{AC}}+\overrightarrow{\text{AD}}$ là một VTPT của (P).

Thử các trường hợp, ta có $(\text{a};\text{b};1-2\text{a})=(1;1;-1)\Rightarrow \left(\text{P}\right):\text{x}+\text{y}-\text{z}-1=0$.

Vậy mặt phẳng (P) đi qua điểm (1;3;3).