Cho hình chóp S.ABC có thể tích bằng a3. Mặt (SBC) vuông góc với đáy. Các cạnh AB=AC=SA=SB=2a . Cạnh SC bằng:

Phương pháp giải:

Gọi H là trung điểm BC, chứng minh H là tâm đường tròn ngoại tiếp tam giác vuông SBC.

Đặt SC = x và giải phương trình tìm x.

Giải chi tiết:

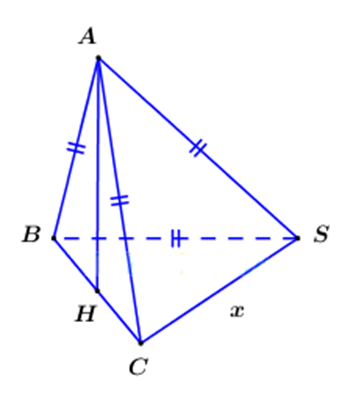
Gọi H là trung điểm $\text{BC.AB}=\text{AC}$ nên $\text{AH}\perp \text{BC}$. Mà $\left(\text{SBC}\right)\perp \left(\text{ABC}\right)$ nên $\text{AH}\perp \left(\text{SBC}\right)$

Vì $\text{AB}=\text{AC}=\text{AS}$ nên H là tâm đường tròn ngoại tiếp tam giác SBC. Suy ra tam giác SBC vuông tại S

Đặt SC $=x>0$, ta có$\begin{array}{l}\text{BC}=\sqrt{{\text{SB}}^2+{\text{SC}}^2}=\sqrt{4{\text{a}}^2+{\text{x}}^2}\\ \text{BH}=\frac{\text{BC}}{2}=\frac{1}{2}\sqrt{4{\text{a}}^2+{\text{x}}^2}=\sqrt{{\text{a}}^2+\frac{{\text{x}}^2}{4}}\\ \text{AH}=\sqrt{{\text{AB}}^2-{\text{BH}}^2}=\sqrt{4{\text{a}}^2-\left({\text{a}}^2+\frac{{\text{x}}^2}{4}\right)}=\sqrt{3{\text{a}}^2-\frac{{\text{x}}^2}{4}}\end{array}$

Từ giả thiết suy ra

$\begin{array}{l}{a}^3=V_{S.ABC}=\frac{1}{3}AH.S_{SBC}=\frac{1}{6}\sqrt{3a^2-\frac{x^2}{4}}.2a.x\iff 6a^2=\sqrt{12a^2-x^2}.x\\ \iff x^4-12a^2{x}^2+36a^4=0\iff {\left(x^2-6a^2\right)}^2=0\iff x^2=6a^2\iff x=a\sqrt{6}\end{array}$