Trong không gian Õyz cho mặt cầu (S): (x-1)^2+y^2+(z-2)^2=10 và hai điểm A(1;2;-4) ;B(1;2;14) . Điểm M(a.b.c) là điểm nằm trên

Phương pháp giải:

Gọi điểm C thỏa mãn MA = 2MC

GTNN của MA + 2MB là BC

Tìm giao của BC với mặt cầu, chính là điểm M cần tìm

Giải chi tiết:

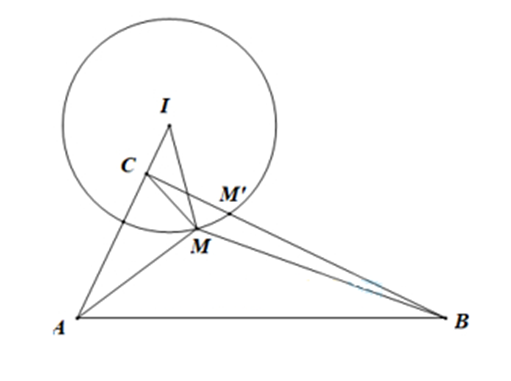
Mặt cầu (S) có tâm $\text{I}(1;0;2)$ và bán kính $\text{R}=\sqrt{10}$. Có

$\overrightarrow{\text{IA}}=(0;2;-6);\text{IA}=\sqrt{2^2+6^2}=2\sqrt{10}=2\text{R}$

Gọi C là điểm thỏa mãn $\overrightarrow{IC}=\frac{1}{4}\overrightarrow{IA}=(0;\frac{1}{2};-\frac{3}{2})\Rightarrow C(1;\frac{1}{2};\frac{1}{2})$ 

Có ${\text{IM}}^2=\text{IC}$. IA $\Rightarrow \Delta \text{IMC}~\Delta \text{IAM}$ (c. g.c)

Đẳng thức xảy ra khi M trùng M ' là giao của đoạn BC với (S)

M’ thuộc đoạn BC $\iff \overrightarrow{CM\text{'}}=k\overrightarrow{CB}=\left(0;\frac{3}{2}k;\frac{27}{2}k\right)(k>0)$ 

$\iff M^{\text{'}}\left(1;\frac{1}{2}+\frac{3}{2}\text{k};\frac{1}{2}+\frac{27}{2}\text{k}\right)$. Ta có

Vậy $a+b+c=7$.