1. Tìm tất cả các giá trị của m để hàm số y=1/3mx^3-(m-1)*x^2+3(m-2)*x+2022 đồng biến trên [2, dương vô cùng).

* Hướng dẫn giải

a) Phương pháp giải:

Hàm số đồng biến khi đạo hàm không âm.

Giải bất phương trình y’ ≥ 0 rồi cô lập m, lập bảng biến thiên trên khoảng cần xét.

Giải chi tiết:

Hàm số đã cho đồng biến trên nửa khoảng đã cho khi và chỉ khi

$y\text{'}=m{x}^2-2(m-1)x+3(m-2)\ge 0\forall x\in [2;+\infty )$ 

$\iff m(x^2-2x+3)\ge 6-2x$ 

$\iff m\ge \frac{6-2x}{x^2-2x+3}(do{x}^2-2x+3={(x-1)}^2+2>0,\forall x)$ 

Xét $f\left(x\right)=\frac{6-2x}{x^2-2x+3}$ trên [2;+∞) có $f\text{'}\left(x\right)=\frac{2x^2-12x+6}{{\left(x^2-2x+3\right)}^2}=0\iff x=3\pm \sqrt{6}$ .

Ta có BBT

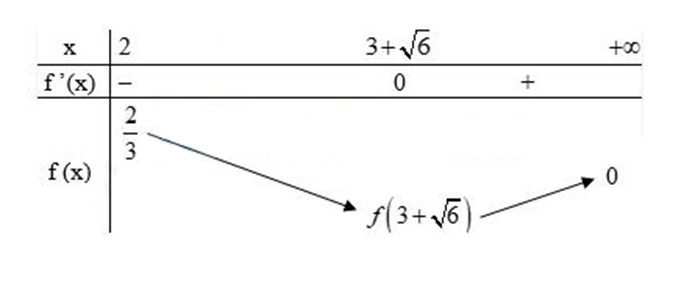
Căn cứ BBT, ta có các giá trị m cần tìm là $m\ge \frac{2}{3}$ 

Vậy $m\ge \frac{2}{3}$.

b) Phương pháp giải:

Tìm số hạng tổng quát của dãy $u_1{u}_2\mathrm{...}{u}_n$.

Từ đó tìm ra $lim\left(u_1{u}_2\mathrm{...}{u}_n\right)$.

Giải chi tiết:

Ta có

$u_n=\frac{n^2+2n}{{\left(n+1\right)}^2}=\frac{n\left(n+2\right)}{{\left(n+1\right)}^2}$ 

$\Rightarrow u_1=\frac{1.3}{2^2};u_2=\frac{2.4}{3^2};\mathrm{...};u_n=\frac{n\left(n+2\right)}{{\left(n+1\right)}^2}$ 

$\Rightarrow u_1{u}_2\mathrm{...}{u}_n=\frac{\mathrm{1.2.3.4...}n\left(n+2\right)}{2^2{.3}^2\mathrm{...}{\left(n+1\right)}^2}=\frac{n+2}{2\left(n+1\right)}$ 

$\Rightarrow \lim \left(u_1{u}_2\mathrm{...}{u}_n\right)=\lim \frac{1+\frac{2}{n}}{2+\frac{2}{n}}=\frac{1}{2}$