Trong không gian với hệ trục tọa độ vuông góc Oxyz, cho mặt phẳng (P): -x+2y+2x-3=0 , mặt cầu (S): X^2+y^2+z^2-10x-4y-6z+2+0

Phương pháp giải:

Tìm tâm I, bán kính R của mặt cầu (S) và vtpt của mặt phẳng (P)

Giải chi tiết:

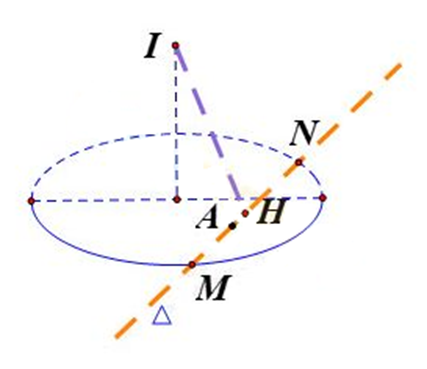
Mặt cầu (S) có tâm I(5;2;3), bán kính $R=\sqrt{5^2+2^2+3^2-2}=6$.

Mặt phẳng (P) có $\overrightarrow{n_{\left(P\right)}}=\left(-1;2;2\right)$ .

Ta có: $d\left(I,\left(P\right)\right)=\frac{\left|-5+2.2+2.3-3\right|}{\sqrt{{\left(-1\right)}^2+2^2+2^2}}=\frac{2}{3}<R$  => Mặt phẳng (P) cắt mặt cầu (S).

$IA=\sqrt{{\left(3-5\right)}^2+{\left(1-2\right)}^2+{\left(2-3\right)}^2}=\sqrt{6}<R$  ⇒ Điểm A nằm trong mặt cầu.

Gọi H là trung điểm của MN. Khi đó IH vuông góc với MN

$=>MN=2HN=2\sqrt{I{N}^2-I{H}^2}=2\sqrt{36-I{H}^2}$ 

Do đó MN min ⇔ IH max

Vì tam giác IAH vuông tại H $\Rightarrow IH\le IA$ 

=> MN min $\iff IH=IA=\sqrt{6}=>MN=2\sqrt{36-6}=2\sqrt{30}$.

Chọn B