Trong không gian với hệ trục tọa độ vuông góc Oxyz, cho đường thẳng d:x/1=(y+1)/2=(z-2)/-1 và mặt phẳng (P): x+y+z=3

Phương pháp giải:

Bước 1: Lấy điểm B(0;−1;2) thuộc d.

Bước 2: Tìm giao điểm A của d và (P)

Bước 3: Gọi H là hình chiếu của B lên (P), B’ là điểm đối xứng B qua (P). Tìm d’

Giải chi tiết:

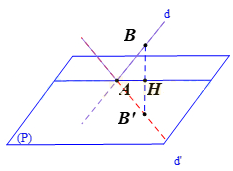
Bước 1: Lấy điểm B(0;−1;2) thuộc d.

Bước 2: Tìm giao điểm A của d và (P)

Gọi A là giao điểm của d và (P).

Khi đó $A\left(t;-1+2t;2-t\right)$. Thay vào (P) ta được: $t-1+2t+2-t-3=0\iff t=1$ 

=> A(1;1;1)

Bước 3: Tìm d’

Gọi H là hình chiếu của B lên (P), B’ là điểm đối xứng B qua (P).

Khi đó H là trung điểm của BB’

Đường thẳng BH đi qua B(0;-1;2) và nhận $\overrightarrow{n_{\left(P\right)}}=\left(1;1;1\right)$ làm vecto chỉ phương có phương trình là: $\left\{\begin{array}{l}x=t\\ y=-1+t\\ z=2+t\end{array}\right.$ 

$\Rightarrow H\left(t;-1+t;2+t\right)$. Thay vào (P) ta được: $t-1+t+2+t-3=0=>t=\frac{2}{3}$

$\Rightarrow H\left(\frac{2}{3};-\frac{1}{3};\frac{8}{3}\right)=>B^{\text{'}}\left(\frac{4}{3};\frac{1}{3};\frac{10}{3}\right)$ 

Vecto chỉ phương của AB’ là: $AB\text{'}=\left(\frac{1}{3};-\frac{2}{3};\frac{7}{3}\right)$ 

Đường thẳng $d^{\text{'}}:\frac{x-1}{1}=\frac{y-1}{-2}=\frac{z-1}{7}$ 

Chọn B