Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc BAD  60. Hình chiếu vuông góc của S lên mặt phẳng đáy

a) Phương pháp giải:

Bước 1: Tính AG.

Bước 2: Xác định góc giữa SA và đáy trên hình.

Bước 3: Tính SG

Bước 4: Tính thể tích S.ABCD.

Giải chi tiết:

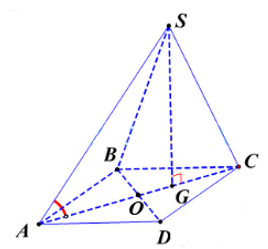
Bước 1: Tính AG.

Gọi O là giao điểm của AC và BD.

ABCD là hình thoi cạnh a nên $BC=CD=a,\angle BAD=\angle BCD={60}^{°}$.

=> Tam giác $B C D$ là tam giác đều  $\Rightarrow CG=\frac{2}{3}\cdot CO=\frac{2}{3}\cdot \frac{\sqrt{3}}{2}BC=\frac{\sqrt{3}}{3}a$

$\Rightarrow AG=2CG=\frac{2\sqrt{3}}{3}a$

Bước 2: Xác định góc giữa SA và đáy trên hình.

Do SG vuông góc với (ABCD) nên góc giữa SA và đáy bằng góc giữa SA và hình chiếu của nó trên (ABCD) tức là góc giữa SA và $\text{GA}\Rightarrow \angle SAG={60}^{°}$.

Bước 3: Tính SG

Tam giác vuông SAG có $\angle SAG={60}^{°}$ nên $SG=AG\sqrt{3}=\frac{2\sqrt{3}}{3}a.\sqrt{3}=2a$

Bước 4: Tính thể tích S.ABCD.

Ta có $AC=3CG=3\cdot \frac{\sqrt{3}}{3}a=a\sqrt{3}$

Diện tích hình thoi ABCD là: $S=\frac{1}{2}.AC.BD=\frac{1}{2}.a\sqrt{3}.a=\frac{a^2\sqrt{3}}{2}$

Thể tích S.ABCD: $V=\frac{1}{3}SG.S_{ABCD}=\frac{1}{3}.2a.\frac{a^2\sqrt{3}}{2}=\frac{a^3\sqrt{3}}{3}$.

b) Phương pháp giải:

Kẻ Bx song song với AC. Kẻ GH vuông góc với Bx, GK vuông góc với SH

Bước 1: Chứng minh GK⊥(SBH)

Bước 2: Chứng minh d(AC,SB)=GK

Bước 3: Tính GK

Giải chi tiết:

 

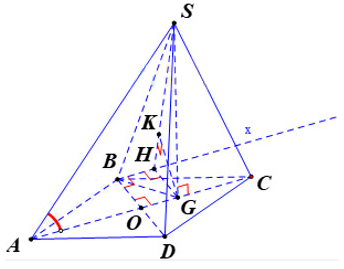
Kẻ Bx song song với AC. Kẻ GH vuông góc với Bx, GK vuông góc với SH

Bước 1: Chứng minh $GK\perp \left(SBH\right)$

Ta có:

$\begin{array}{l}\left\{\begin{array}{l}GH\perp BH\\ BH\perp SG\end{array}\Rightarrow BH\perp \left(SGH\right)\Rightarrow BH\perp GK\right.\\ \left\{\begin{array}{l}BH\perp GK\\ GK\perp SH\end{array}\Rightarrow GK\perp \left(SHB\right)\right.\end{array}$

Bước 2: Chứng minh $d(AC,SB)=GK$

Ta có $\text{BH}//\text{AC}\Rightarrow AC//\left(SHB\right)$

Mà $SB\subset \left(SHB\right)\Rightarrow d(SB,AC)=d(AC,(SHB\left)\right)=d(G,(SHB\left)\right)=GK$

Bước 3: Tính GK

Dễ thấy tứ giác OBHG là hình chữ nhật $\Rightarrow HG=OB=\frac{a}{2}$.

Áp dụng hệ thức lượng trong tam giác vuông SGH ta có:

$\frac{1}{G{K}^2}=\frac{1}{S{G}^2}+\frac{1}{G{H}^2}=\frac{1}{4a^2}+\frac{4}{a^2}=\frac{17}{4a^2}\Rightarrow GK=\frac{2\sqrt{17}a}{17}$

Vậy $d(SB,AC)=\frac{2a\sqrt{17}}{17}$