Trong hình vẽ, xe A kéo xe B bằng một sợi dây dài 39m qua một ròng rọc ở độ cao 12m. Xe A xuất phát từ N và chạy với vận tốc
Câu hỏi :
Trong hình vẽ, xe A kéo xe B bằng một sợi dây dài 39m qua một ròng rọc ở độ cao 12m. Xe A xuất phát từ N và chạy với vận tốc không đổi 2 m/s theo chiều mũi tên.
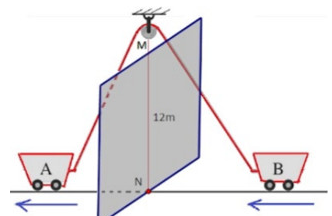
a) Đặt và , (đơn vị mét). Tìm một hệ thức liên hệ giữa x và y .
b) Tính vận tốc của xe B khi xe A cách N một đoạn 5m.
Trong hình vẽ, xe A kéo xe B bằng một sợi dây dài 39m qua một ròng rọc ở độ cao 12m. Xe A xuất phát từ N và chạy với vận tốc không đổi 2 m/s theo chiều mũi tên.

a) Đặt và , (đơn vị mét). Tìm một hệ thức liên hệ giữa x và y .
b) Tính vận tốc của xe B khi xe A cách N một đoạn 5m.
* Đáp án
* Hướng dẫn giải
a) Phương pháp giải:
Coi M, A, B là một tam giác và N thuộc cạnh AB
Bước 1: Xác định AM+BMAM+BM, MN
Bước 2: Tìm mối liên hệ giữa x và y.
Giải chi tiết:
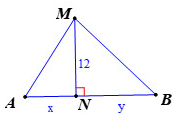
Bước 1: Xác định AM + BM, MN
Coi M,A,B là một tam giác và N thuộc cạnh AB
Sợi dây dài .
Có MN=12.
Bước 2: Tìm mối liên hệ giữa ![]() và y.
và y.
Theo định lý py-ta-go ta được:
Vậy hệ thức cần tìm là
b) Phương pháp giải:
Gọi t là thời gian xe A di chuyển.
Bước 1: Tìm mối quan hệ giữa x và t
Bước 2: Tìm mối quan hệ giữa y và t
Bước 3: Tính quãng đường tại t=2,5(s).
Giải chi tiết:
Bước 1: Tìm mối quan hệ giữa x và t
Khi A sang trái thì x tăng dần và y giảm dần
Tạo mối quan hệ giữa y và t
Vì xe A chuyển động đều với vận tốc là 2m/s nên mối quan hệ giữa x và t là:
Bước 2: Tìm mối quan hệ giữa y và t
Mà ta có nên:
Quãng đường A đi được là 5m nên ta có t=2,5(s)
Bước 3: Tính quãng đường tại t=2,5(s)
Vận tốc tại thời điểm t=2,5(s) của B là y′(2,5). Khi đó
Vậy .
Vận tốc tức thời của xe B tại thời điểm xe A cách N 5m là -0,867(m/s).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi Đánh giá tư duy Đọc hiểu, Toán học có đáp án !!
Copyright © 2021 HOCTAP247
