Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại B và AC = 2a biết rằng (A'BC) hợp với đáy (ABC)

* Hướng dẫn giải

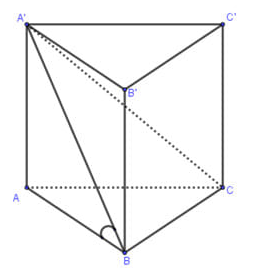
Tam giác \(ABC\) là tam giác vuông cân tại \(B.\) Gọi \(BA = BC = b.\)

Áp dụng định lí Pitago vào trong tam giác vuông \(ABC\) ta có \(\sqrt {B{A^2} + B{C^2}} = AC \Leftrightarrow b\sqrt 2 = 2a \Leftrightarrow b = a\sqrt 2 .\)

Diện tích đáy là \({S_{ABC}} = \frac{1}{2}BA.BC = \frac{1}{2}{b^2} = \frac{1}{2}{\left( {a\sqrt 2 } \right)^2} = {a^2}.\)

Ta có \(\left\{ \begin{array}{l}\left( {A'BC} \right) \cap \left( {ABC} \right) = BC\\BC \bot \left( {AA'B} \right)\\\left( {AA'B} \right) \cap \left( {ABC} \right) = AB\\\left( {AA'B} \right) \cap \left( {A'BC} \right) = A'B\end{array} \right..\) Do đó góc giữa \(\left( {A'BC} \right)\) và đáy \(\left( {ABC} \right)\) bằng góc giữa \(AB\) và \(A'B\) và bằng góc \(\widehat {ABA'},\) theo giả thiết, ta có \(\widehat {ABA'} = {45^0}.\)

Tam giác \(AA'B\) vuông cân tại \(A\) nên \(AA' = AB = a\sqrt 2 .\)

Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng \(V = AA'.{S_{ABC}} = a\sqrt 2 .{a^2} = {a^3}\sqrt 2 .\)

Đáp án D