Cho hàm số y = f(x). Khẳng định nào sau đây là đúng?
Câu hỏi :
Cho hàm số \(y = f(x)\). Khẳng định nào sau đây là đúng?
A. Nếu hàm số \(y = f(x)\) đạt cực trị tại \({x_0}\) thì \(f''({x_0}) >0\) hoặc \(f''({x_0}) < 0\) .
B. Nếu \(f'({x_0}) = 0\) thì hàm số \(y = f(x)\) đạt cực trị tại \({x_0}\).
C. Nếu hàm số \(y = f(x)\) đạt cực trị tại \({x_0}\) thì nó không có đạo hàm tại \({x_0}\) .
D. Nếu hàm số đạt cực trị tại \({x_0}\) thì hàm số không có đạo hàm tại \({x_0}\) hoặc \(f'({x_0}) = 0\) .
* Đáp án
D
* Hướng dẫn giải
Phương án A và C sai vì: Chọn hàm số \(y = {x^4}.\)
Tập xác định \(D = \mathbb{R}.\)
Ta có \(y' = 4{x^3},\) cho \(y' = 0 \Leftrightarrow 4{x^3} = 0 \Leftrightarrow x = 0.\)
Và
Bảng biến thiên
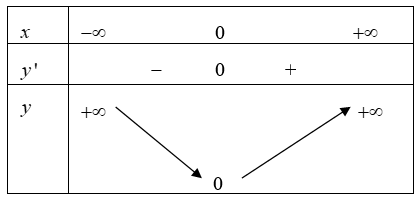
Hàm số \(y = {x^4}\) đạt cực trị tại \(x = 0\) nhưng và có đạo hàm tại \(x = 0.\)
Tập xác định \(D = \mathbb{R}.\)
Ta có \(y' = 3{x^2},\) cho \(y' = 0 \Leftrightarrow 3{x^2} = 0 \Leftrightarrow x = 0,\)
Bảng biến thiên
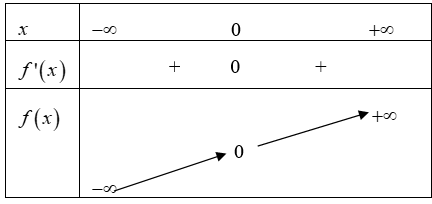
Hàm số không đạt cực trị tại \(x = 0.\)
Đáp án D
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
[Năm 2022] Đề thi thử môn Toán THPT Quốc gia có đáp án (30 đề) !!
Copyright © 2021 HOCTAP247
