Cho lăng trụ đứng ABC.A'B'C' có [AB = AC = BB' = a; góc BAC = 120^0. Gọi I là trung điểm của CC'. Côsin của góc tạo

* Hướng dẫn giải

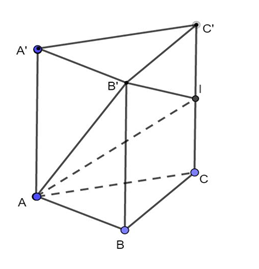
Gọi \(\alpha \) là góc tạo bởi hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {AB'I} \right).\)

Do tam giác \(ABC\) là hình chiếu của tam giác \(AB'I\) trên mặt phẳng \(\left( {ABC} \right)\) nên ta có

\({S_{ABC}} = {S_{AB'I}}.\cos \alpha \)

\({S_{ABC}} = \frac{1}{2}.AB.AC.\sin {120^0} = \frac{{{a^2}\sqrt 3 }}{4}.\)

\(AB{'^2} = AA{'^2} + A'B{'^2} = 2{a^2}.\)

\(A{I^2} = A{C^2} + C{I^2} = {a^2} + \frac{{{a^2}}}{4} = \frac{{5{a^2}}}{4}\)

\(C'B{'^2} = C'A{'^2} + A'B{'^2} - 2.A'B'.A'C'.\cos {120^0} = 3{a^2}.\)

\(B'{I^2} = B'C{'^2} + C'{I^2} = 3{a^2} + \frac{{{a^2}}}{4} = \frac{{13{a^2}}}{4}.\)

Có \(AB{'^2} + A{I^2} = B'{I^2} \Rightarrow \Delta AB'I\) vuông tại \(A.\)

\({S_{AB'I}} = \frac{1}{2}.AB'.AI = \frac{{{a^2}\sqrt {10} }}{4}.\) Do đó \(\cos \alpha = \frac{{{S_{ABC}}}}{{{S_{AB'I}}}} = \frac{{\sqrt {30} }}{{10}}.\)

Đáp án D