Cho hàm số f(x) có đạo hàm liên tục trên R và f(0)= 0, f(4) lớn hơn 4
Câu hỏi :
Cho hàm số f(x) có đạo hàm liên tục trên R và , . Biết hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số là?
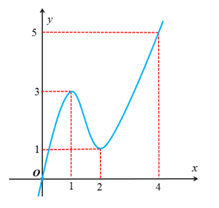
Cho hàm số f(x) có đạo hàm liên tục trên R và , . Biết hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số là?

* Đáp án
D
* Hướng dẫn giải
Đáp án D
Nhắc lại: Số cực trị hàm số được tính bằng tổng số cực trị hàm số f(x) và giao điểm của hàm số f(x) với trục hoành.
Ta có
Xét (1)
Nếu thì phương trình (1) vô nghiệm
Nếu đặt thì (1) trở thành (2)
Vẽ đồ thị hai hàm số , trên cùng một hệ trục tọa độ.
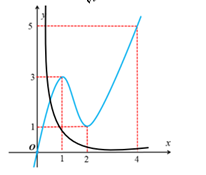
Quan sát hai đồ thị ta thấy
- Nếu thì hàm số f '(t) đồng biến, còn hàm số nghịch biến nên (2) có nghiệm duy nhất .
- Nếu thì nên (2) vô nghiệm.
Từ các nhận xét trên ta có bảng biến thiên
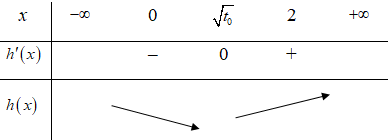
Ta có . Nên hàm số h(x) có một điểm cực tiểu và cắt trục hoành tại hai điểm phân biệt. Từ đó ta có có 3 cực trị.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Copyright © 2021 HOCTAP247
