Cặp bất phương trình nào sau đây là tương đương?

* Hướng dẫn giải

Đặt \[f\left( x \right) = {x^2}\left( {x - 2} \right).\]

Phương trình \[{x^2} = 0 \Leftrightarrow x = 0\] và\[x - 2 = 0 \Leftrightarrow x = 2.\]

Lập bảng xét dấu

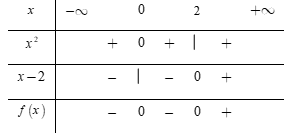
Dựa vào bảng xét dấu ta thấy:

+) Đáp án A: \[x - 2 \le 0 \Leftrightarrow x \le 2\]  và\[{x^2}\left( {x - 2} \right) \le 0 \Leftrightarrow x \le 2\] nên hai bất phương trình tương đương. Chọn A.

+) Đáp án B: \[x - 2 0 \Leftrightarrow x >2\]  nên hai bất phương trình không tương đương. Loại B.>

+) Đáp án C: \[x - 2

+) Đáp án D:\[{x^2}(x - 2) \ge 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x \ge 2}\end{array}} \right.\] và \[x - 2 \ge 0 \Leftrightarrow x \ge 2\] nên hai bất phương trình không tương đương. Loại D.

Đáp án cần chọn là: A