Tập nghiệm SS của bất phương trình

* Hướng dẫn giải

Điều kiện: \[{x^2} - 3x - 10 \ne 0 \Leftrightarrow (x + 2)(x - 5) \ne 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \ne - 2}\\{x \ne 5}\end{array}} \right.\]

Bất phương trình\[\frac{{ - \,2{x^2} + 7x + 7}}{{{x^2} - 3x - 10}} \le - 1 \Leftrightarrow \frac{{ - 2{x^2} + 7x + 7}}{{{x^2} - 3x - 10}} + 1 \le 0 \Leftrightarrow \frac{{ - {x^2} + 4x - 3}}{{{x^2} - 3x - 10}} \le 0\,\,\,\,\left( * \right)\]

Bảng xét dấu

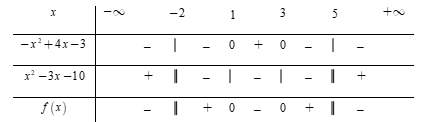
Dựa vào bảng xét dấu, bất phương trình \[\left( * \right) \Leftrightarrow x \in \left( { - \,\infty ; - \,2} \right) \cup \left[ {1;3} \right] \cup \left( {5; + \,\infty } \right).\]Đáp án cần chọn là: C