Tập nghiệm của bất phương trình

* Hướng dẫn giải

Đặt \[f\left( x \right) = 2x\left( {4 - x} \right)\left( {3 - x} \right)\left( {3 + x} \right).\]

Phương trình \[2x = 0 \Leftrightarrow x = 0;\,\,4 - x = 0 \Leftrightarrow x = 4;\,\,\]

Và\[3 - x = 0 \Leftrightarrow x = 3;3 + x = 0 \Leftrightarrow x = - 3\]

Ta có bảng xét dấu:

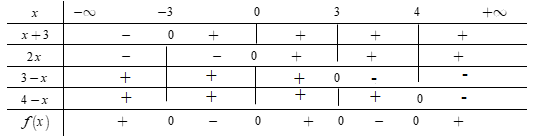
Từ bảng xét dấu ta có

\[f(x) >0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x >4}\\{0 < x < 3}\\{x < - 3}\end{array}} \right. \Leftrightarrow x \in ( - \infty ; - 3) \cup (0;3) \cup (4; + \infty ).\]

Suy ra tập nghiệm bất phương trình là hợp của ba khoảng.

Đáp án cần chọn là: C