Bất phương trình (x + 4)/( x^2 − 9 )− 2/(x + 3) < 4x/ (3x − x^2)

* Hướng dẫn giải

Bất phương trình tương đương với

\[\frac{{x\left( {x + 4} \right)}}{{x\left( {x - 3} \right)\left( {x + 3} \right)}} - \frac{{2x\left( {x - 3} \right)}}{{x\left( {x - 3} \right)\left( {x + 3} \right)}} < - \frac{{4x\left( {x + 3} \right)}}{{x\left( {x - 3} \right)\left( {x + 3} \right)}} \Leftrightarrow \frac{{3x + 22}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} < 0.\]

Đặt \[f\left( x \right) = \frac{{3x + 22}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}.\]

Ta có \[3x + 22 = 0 \Leftrightarrow x = - \frac{{22}}{3};\left\{ {\begin{array}{*{20}{c}}{x - 3 = 0 \Leftrightarrow x = 3}\\{x + 3 = 0 \Leftrightarrow x = - 3}\end{array}} \right.\]

Bảng xét dấu

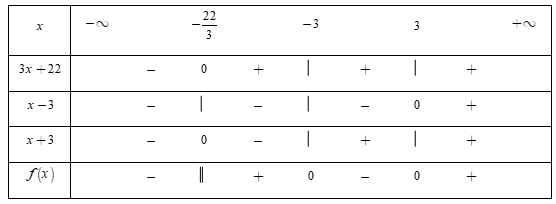
Dựa vào bảng xét dấu, ta thấy rằng\[f\left( x \right) < 0 \Leftrightarrow x \in \left( { - \,\infty ; - \frac{{22}}{3}} \right) \cup \left( { - \,3;3} \right).\]

Vậy nghiệm nguyên lớn nhất thỏa mãn bất phương trình là x = 2.

Đáp án cần chọn là: A