Trong không gian Oxyz, cho ba mặt phẳng (P): x-2y+z-1=0, (Q):x-2y+z+8=0

Đáp án C

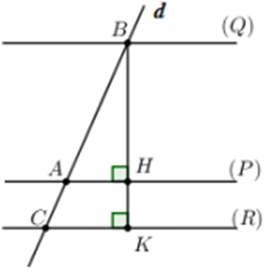
Ta có \[\left( P \right),\left( Q \right),\left( R \right)\] đôi một song song và \[\left( P \right)\] nằm giữa \[\left( Q \right),\left( R \right)\].

Kẻ \[BH \bot \left( P \right),BK \bot \left( R \right) \Rightarrow B,H,K\] thẳng hàng.

Điểm \[M\left( {0;0; - 8} \right) \in \left( Q \right).BH = d\left( {M;\left( P \right)} \right) = 3;BK = d\left( {M;\left( R \right)} \right) = 4 \Rightarrow HK = 1\]

Ta có \[\frac{{AB}}{{AC}} = \frac{{BH}}{{HK}} = 3 \Rightarrow AB = 3AC\]

$\Rightarrow T=9A{C}^2+\frac{144}{A{C}^2}\ge 2\sqrt{9A{C}^2.\frac{144}{A{C}^2}}=72$

Dấu “=” xảy ra \[ \Leftrightarrow AC = 2\](thỏa mãn \[AC > HK = 1\]). Chọn C.