Cho hàm số y=f(x) liên tục trên R và có bảng biến thiên như sau:

Đáp án C

Đặt \[t = {x^3} - 3{x^2}\], ta có \[t' = 3{x^2} - 6x;t' = 0\left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\]

Bảng biến thiên (1):

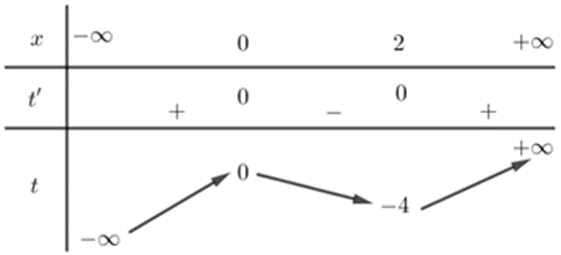
Phương trình đã cho trở thành $\left|f\left(t\right)\right|=\frac{3}{2}\iff \left[\begin{array}{l}f\left(t\right)=\frac{3}{2}\\ f\left(t\right)=-\frac{3}{2}\end{array}\right.$

Từ giả thiết, ta có bảng biến thiên (2) của hàm số \[y = f\left( x \right)\]:

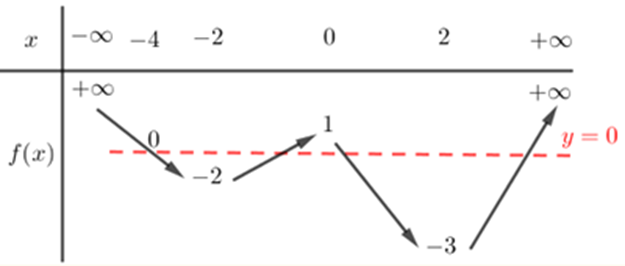
Dựa vào bảng biến thiên (2), ta có

+) $f\left(t\right)=\frac{3}{2}\iff \left[\begin{array}{l}t=t_1\left(t_1<-4\right)\left(1.1\right)\\ t=t_2\left(t_2>2\right)\left(1.2\right)\end{array}\right.$. Dựa vào bảng biến thiên (1), ta có phương trình (1.1) có 1 nghiệm và phương trình (1.2) có 1 nghiệm (các nghiệm này không trùng nhau).

$f\left(t\right)=-\frac{3}{2}\iff \left[\begin{array}{l}t=t_3\left(-4<t_3<-2\right),\left(2.1\right)\\ t=t_4\left(-2<t_4<0\right),\left(2.2\right)\\ t=t_5\left(0<t_5<2\right),\left(2.3\right)\\ t=t_6\left(t_6>2\right),\left(2.4\right)\end{array}\right.$

Dựa vào bảng biến thiên (1), ta có phương trình (2.1) có 3 nghiệm; phương trình (2.2) có 3 nghiệm; phương trình (2.3) có 1 nghiệm; phương trình (2.4) có 1 nghiệm (các nghiệm này không trùng nhau và không trùng với các nghiệm của phương trình \[f\left( t \right) = \frac{3}{2}\]).

Vậy phương trình đã cho có 10 nghiệm.