Cho khối nón (N) đỉnh S, có chiều cao là a căn bậc hai của 3 và độ dài đường sinh là 3a

Đáp án A

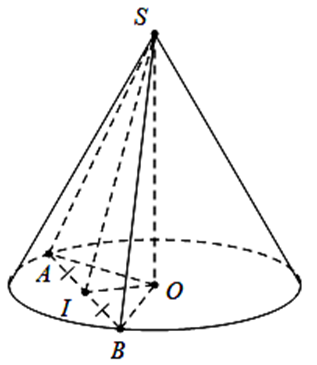
Khối nón (N) có tâm đáy là O, chiều cao \(SO = h = a\sqrt 3 \) và độ dài đường sinh \(\ell  = 3{\rm{a}}\).

Giả sử mặt phẳng (P) cắt (N) theo thiết diện là tam giác SAB.

Do \(SA = SB = \ell  \Rightarrow \Delta SAB\) cân tại đỉnh S.

Gọi I là trung điểm của AB. Ta có: \(OI \bot AB,SI \bot AB\) và khi đó góc giữa mặt phẳng (P) và mặt đáy (N) là góc \(\widehat {SI{\rm{O}}} = 60^\circ \).

Trong tam giác SOI vuông tại O góc \(\widehat {SI{\rm{O}}} = 60^\circ \).

Ta có: \(SI = \frac{{SO}}{{\sin SIO}} = \frac{{a\sqrt 3 }}{{\sin 60^\circ }} = 2a\).

Trong tam giác SIA ta có: \(I{A^2} = S{A^2} - S{I^2} = 5{{\rm{a}}^2} \Rightarrow IA = a\sqrt 5 \).

\(AB = 2IA = 2{\rm{a}}\sqrt 5 \). Vậy diện tích thiết diện cần tìm là:

\({S_{t{\rm{d}}}} = {S_{SAB}} = \frac{1}{2}SI.AB = 2{{\rm{a}}^2}\sqrt 5 \).