Cho hàm số y=f(x) có đạo hàm trên R và hàm y=f'(x) có đồ thị như hình vẽ.

Đáp án D

Ta có \(g\left( x \right) = f\left( {\frac{x}{2} + 1} \right) - \ln {\left( {x + 4} \right)^2} = f\left( {\frac{x}{2} + 1} \right) - 2\ln \left( {x + 4} \right){\rm{ }}\left( {x \in \left[ { - 3;4} \right]} \right)\).

\(g'\left( x \right) = \frac{1}{2}f'\left( {\frac{x}{2} + 1} \right) - \frac{2}{{x + 4}};{\rm{ g'}}\left( x \right) = 0 \Leftrightarrow f'\left( {\frac{x}{2} + 1} \right) = \frac{4}{{x + 4}}\).

Đặt \(\frac{x}{2} + 1 = t \Rightarrow x = 2t - 2\), khi đó phương trình có dạng \(f'\left( t \right) = \frac{2}{{t + 1}}/\left[ { - \frac{1}{2};3} \right]\) (*):

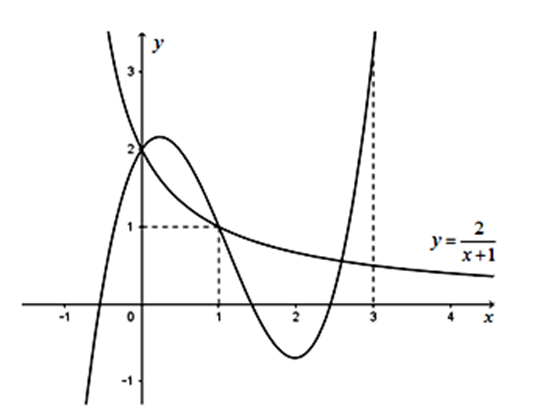
Số điểm cực trị của hàm số \(g\left( x \right) = f\left( {\frac{x}{2} + 1} \right) - \ln \left( {{x^2} + 8{\rm{x}} + 16} \right)\) là số nghiệm đơn (hay bội lẻ) của phương trình (*) trên \(\left[ { - \frac{1}{2};3} \right]\). Từ đồ thị hàm số trên ta suy ra hàm số có 3 điểm cực trị.