Cho hàm số y=f(x) có bảng biến thiên sau. Tìm giá trị nhỏ nhất của hàm số

Đáp án A

Ta có \(g'\left( x \right) = \left( {3{{\rm{x}}^2} - 3} \right)f'\left( {{x^3} - 3{\rm{x}}} \right) - {x^4} + 5{{\rm{x}}^2} - 4\)

\( = \left( {{x^2} - 1} \right)\left[ {3f'\left( {{x^3} - 3{\rm{x}}} \right) + 4 - {x^2}} \right]\).

Với \(x \in \left[ { - 1;2} \right] \Rightarrow {x^3} - 3{\rm{x}} \in \left[ { - 2;2} \right]\) nên \(f'\left( {{x^2} - 3{\rm{x}}} \right) > 0,\forall x \in \left[ { - 2;2} \right]\).

Và \(x \in \left[ { - 1;2} \right]\) thì \(4 - {x^2} \ge 0\) nên \(f'\left( {{x^3} - 3{\rm{x}}} \right) + 4 - {x^2} > 0,\forall x \in \left[ { - 1;2} \right]\).

Do đó $g^{\text{'}}\left(x\right)=0\iff x^2-1=0\iff \left[\begin{array}{l}x=-1\\ x=1\end{array}\right.$

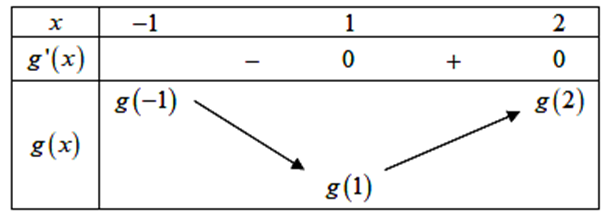
Dựa vào bảng biến thiên, ta được $\underset{\left[-1;2\right]}{\min }g\left(x\right)=g\left(1\right)=f\left(-2\right)-3=-19$