Cho hình nón (N) có đường cao bằng a căn bậc hai cảu 3 , đáy của (N) có bán kính bằng

Đáp án C

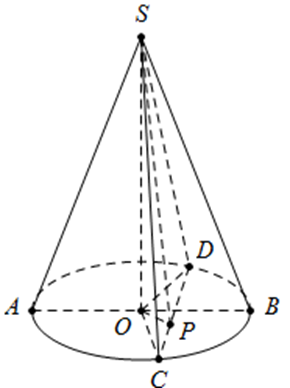
Thiết diện qua đỉnh của \[\left( N \right)\] là \[\Delta SCD\] như hình vẽ.

\[\begin{array}{l}S{C^2} = S{O^2} + O{C^2} = 3{a^2} + {a^2} \Rightarrow SC = 2a.\\S{D^2} = S{O^2} + O{D^2} = 3{a^2} + {a^2} \Rightarrow SD = 2a.\end{array}\]

Bài ra có chu vi \[\Delta SCD\] bằng 5a

 \[ \Rightarrow SC + SD + CD = 5a \Rightarrow 4a + CD = 5a \Rightarrow CD = a\].

Kẻ \[SP \bot CD\] mà \[SC = SD = 2a\].

\[\begin{array}{l} \Rightarrow PC = PD = \frac{{CD}}{2} = \frac{a}{2} \Rightarrow S{P^2} = S{C^2} - C{P^2} = 4{a^2} - \frac{{{a^2}}}{4}\\ \Rightarrow SP = \frac{{a\sqrt {15} }}{2} \Rightarrow {S_{SCD}} = \frac{1}{2}CD.SP = \frac{1}{2}a.\frac{{a\sqrt {15} }}{2} = \frac{{{a^2}\sqrt {15} }}{4}.\end{array}\]