Có bao nhiêu số nguyên m lớn hơn để hàm số f(x)=x^3/3+mx^2+3x+5m-1

Đáp án C

Ta có \[f'\left( x \right) = {x^2} + mx + 3\].

Hàm số nghịch biến trên khoảng \[\left( {1;3} \right) \Leftrightarrow f'\left( x \right) \le 0\;\forall x \in \left( {1;3} \right)\].

$\begin{array}{l}\iff x^2+mx+3\le 0\forall x\in \left(1;3\right)\\ \iff m\le -x-\frac{3}{x}=g\left(x\right)\forall x\in \left(1;3\right)\\ g\text{'}\left(x\right)=\frac{-x^2+3}{x^2};g\text{'}\left(x\right)=0\iff x=\pm \sqrt{3}\end{array}$

Bảng biến thiên:

$m\le g\left(x\right)\forall x\in \left(1;3\right)\iff m\le \underset{\left[1;3\right]}{\min }g\left(x\right)\iff m\le -4$

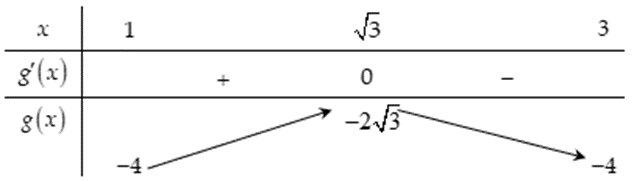
Vậy \[m \in \left\{ { - 9; - 8; - 7; - 6; - 5; - 4} \right\}\].