Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với (ABCD) và SA=2a. Gọi G là trọng tâm tam giác SAB,

* Hướng dẫn giải

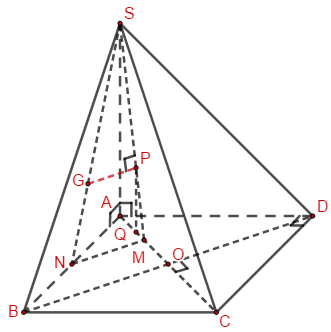
Bước 1:

Gọi O là tâm của ABCD.

M là trung điểm của AO, N là trung điểm của AB.

Qua G kẻ GP song song với MN \[(P \in SM).\]

Ta có ABCD là hình vuông nên \[BD \bot AC\]. Mà \[MN||BD \Rightarrow MN \bot AC\].

Ta lại có \[MN \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)\]

\[\begin{array}{l}MN \bot \left( {SAC} \right)\\GP||MN \Rightarrow GP \bot \left( {SAC} \right)\end{array}\]

Bước 2:

Hình chiếu của C lên (SAC) là C, hình chiếu của G lên (SAC) là P.

=> Hình chiếu của CG lên (SAC) là CP

Góc giữa CG và (SAC) là góc giữa CG và CP và bằng \[\widehat {GCP} = \alpha \]

Bước 3:

\[GP = \frac{2}{3}MN = \frac{2}{3}.\frac{1}{2}OB = \frac{1}{3}.\frac{1}{2}BD = \frac{1}{6}.a\sqrt 2 \]

Kẻ\[PQ||SA \Rightarrow PQ = \frac{1}{3}SA = \frac{{2a}}{3}\]

\[\begin{array}{*{20}{l}}{CQ = \frac{1}{3}MA + 3MA = \frac{{10}}{3}.MA}\\{ = \frac{{10}}{3}.\frac{1}{4}AC = \frac{5}{6}AC = \frac{{5.a\sqrt 2 }}{6}}\\{ \Rightarrow CP = \sqrt {C{Q^2} + P{Q^2}} }\\{ = \sqrt {\frac{{25{a^2}}}{{18}} + \frac{{4{a^2}}}{9}} = a\sqrt {\frac{{11}}{6}} }\\{ \Rightarrow CG = \sqrt {C{P^2} + G{P^2}} = \frac{{a\sqrt {17} }}{3}}\\{ \Rightarrow \sin \alpha = \frac{{GP}}{{CG}} = \frac{{\sqrt 2 }}{6}.\frac{3}{{\sqrt {17} }} = \frac{1}{{\sqrt {34} }}}\end{array}\]

Đáp án cần chọn là: B