Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, cạnh a, góc
Câu hỏi :
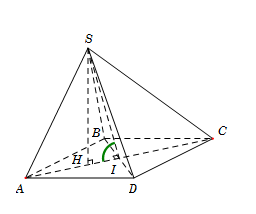
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, cạnh a, góc \(\widehat {BAD} = {60^0},SA = SB = SD = \frac{{a\sqrt 3 }}{2}\). Gọi \[\varphi \] là góc giữa hai mặt phẳng (SBD) và (ABCD). Mệnh đề nào sau đây đúng?
A.\[\tan \varphi = \sqrt 5 .\]
B. \[\tan \varphi = \frac{{\sqrt 5 }}{5}.\]
C. \[\tan \varphi = \frac{{\sqrt 3 }}{2}.\]
D. \[\varphi = {45^0}.\]
* Đáp án
* Hướng dẫn giải
Từ giả thiết suy ra tam giác ABD đều cạnh aa.
Gọi H là hình chiếu của SS trên mặt phẳng (ABCD).
Do SA=SB=SD nên suy ra H là tâm của tam gác đều ABD.
Suy ra
\[AH = \frac{2}{3}AI = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3},HI = \frac{1}{3}AI = \frac{1}{3}\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{6}\]
và\[SH = \sqrt {S{A^2} - A{H^2}} = \frac{{a\sqrt {15} }}{6}.\]
Vì ABCD là hình thoi nên \[HI \bot BD\]. Tam giác SBD cân tại S nên\[SI \bot BD\]. Do đó\[\widehat {\left( {SBD} \right);\left( {ABCD} \right)} = \widehat {\left( {SI;AI} \right)} = \widehat {SIH}.\]
Trong tam vuông SHI, có\[\tan \widehat {SIH} = \frac{{SH}}{{HI}} = \sqrt 5 .\]
Đáp án cần chọn là: A
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Góc giữa hai mặt phẳng !!
Copyright © 2021 HOCTAP247
