Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB=AC=a. Hình chiếu vuông góc HH của SS trên mặt đáy (ABC) trùng với tâm đường tròn ngoại tiếp tam giác ABC và

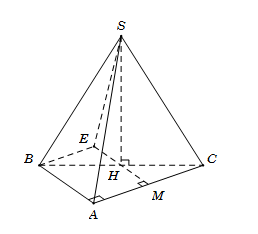
Gọi H là trung điểm BC. Tam giác ABC vuông tại A nên H trung điểm của BC.

Theo giả thiết, ta có \[SH \bot \left( {ABC} \right)\]

Qua B kẻ\[Bx//AC\] . Khi đó \[\widehat {\left( {SB;AC} \right)} = \widehat {\left( {SB;Bx} \right)}\]

Kẻ\[HE \bot Bx\]  tại E, cắt AC tại M

Suy ra AMEB là hình chữ nhật nên\(\left\{ {\begin{array}{*{20}{c}}{BE = AM = \frac{1}{2}AC = \frac{a}{2}}\\{HE = HM = \frac{1}{2}AB = \frac{a}{2}}\end{array}} \right.\)

Ta có\(\left\{ {\begin{array}{*{20}{c}}{Bx \bot HE}\\{Bx \bot SH}\end{array}} \right. \Rightarrow Bx \bot (SHE) \Rightarrow Bx \bot SE\)

Tam giác vuông SEB vuông tại E, có\[\cot \widehat {SBE} = \frac{{BE}}{{SE}} = \frac{{AM}}{{\sqrt {S{H^2} + H{E^2}} }} = \frac{{\frac{a}{2}}}{{\sqrt {\frac{{6{a^2}}}{4} + \frac{{{a^2}}}{4}} }} = \frac{{\sqrt 7 }}{7}\]