Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và AC=AD=BC=BD=a,CD=2x. Với giá trị nào của x thì hai mặt phẳng (ABC) và (ABD) vuông góc. Gọi M,N lần lượt là...

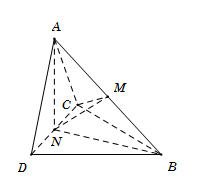
Gọi M,N lần lượt là trung điểm của AB,CD.

Ta có \[AN \bot CD\] mà\[\left( {ACD} \right) \bot \left( {BCD} \right)\]

\[ \Rightarrow AN \bot \left( {BCD} \right) \Rightarrow AN \bot BN \Rightarrow {\rm{\Delta }}ANB\] vuông tại N \[ \Rightarrow NM = \frac{{AB}}{2}\,\,\left( 1 \right)\]Tam giác ABC cân tại C, có M là trung điểm của AB \[ \Rightarrow CM \bot AB.\]

Giả sử \[\left( {ABC} \right) \bot \left( {ABD} \right)\]mà\[CM \bot AB \Rightarrow CM \bot \left( {ABD} \right) \Rightarrow CM \bot DM.\]

Khi đó, \[{\rm{\Delta }}\,MCD\] vuông tại M. Ta có

\[{\rm{\Delta }}ABC = {\rm{\Delta }}ABD\,\,\left( {c.c.c} \right) \Rightarrow CM = DM \Rightarrow {\rm{\Delta }}MCD\] vuông cân tại M.

\[ \Rightarrow \,\,MN = \frac{{CD}}{2}\,\,\,\left( 2 \right)\]Từ (1) và (2)\[ \Rightarrow AB = CD = 2x\]

Lại có

\[{\rm{\Delta }}ACD = {\rm{\Delta }}BCD\,\,\left( {c.c.c} \right) \Rightarrow AN = BN = \sqrt {A{C^2} - C{N^2}} = \sqrt {{a^2} - {x^2}} ,\]

mà\[A{B^2} = A{N^2} + B{N^2}.\]

Suy ra\[2\left( {{a^2} - {x^2}} \right) = 4{x^2} \Leftrightarrow {a^2} = 3{x^2} \Leftrightarrow x = \frac{{a\sqrt 3 }}{3}.\]