Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C. Gọi H là trung điểm AB. Biết rằng SH vuông góc với mặt phẳng (ABC) và AB=SH=a. Tính cosin của góc α tọa bởi hai mặt phẳn...

* Hướng dẫn giải

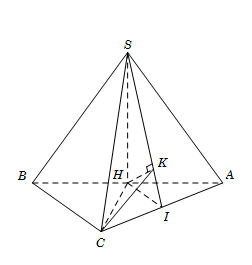
Ta có \[SH \bot \left( {ABC} \right) \Rightarrow SH \bot CH\](1)

Tam giác ABC cân tại C nên \[CH \bot AB\](2)

Từ (1) và (2), suy ra\[CH \bot \left( {SAB} \right)\]

Gọi I là trung điểm \[AC \Rightarrow \,\,HI//BC\mathop \to \limits^{BC{\kern 1pt} \bot {\kern 1pt} {\kern 1pt} AC} HI \bot AC\](3)

Mặt khác\[AC \bot SH\] (do \[SH \bot \left( {ABC} \right)\])(4)

Từ (3) và (4), suy ra \[AC \bot \left( {SHI} \right)\]

Kẻ\[HK \bot SI\,\left( {K \in SI} \right)\](5)

Từ \[AC \bot \left( {SHI} \right) \Rightarrow AC \bot HK\](6)

Từ (5) và (6), suy ra \[HK \bot \left( {SAC} \right)\]

Vì\(\left\{ {\begin{array}{*{20}{c}}{HK \bot (SAC)}\\{HC \bot (SAB)}\end{array}} \right.\) nên góc giữa hai mặt phẳng (SAC) và (SAB) bằng góc giữa hai đường thẳng HK và HC

Ta có \[HK \bot \left( {SAC} \right) \Rightarrow HK \bot CK \Rightarrow {\rm{\Delta }}CHK\] vuông tại KDo đó góc giữa hai mặt phẳng (SAC) và (SAB) là\[\widehat {CHK}\]Có\[CH = \frac{1}{2}AB = \frac{a}{2}\]

\[\frac{1}{{H{K^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{I^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{{\left( {\frac{1}{2}.\frac{a}{{\sqrt 2 }}} \right)}^2}}} \Rightarrow HK = \frac{a}{3}\]

Do đó\[\cos \widehat {CHK} = \frac{{HK}}{{CH}} = \frac{{\frac{a}{3}}}{{\frac{a}{2}}} = \frac{2}{3}.\]Đáp án cần chọn là: D